Ordinary Differential Equations | Mathematics - Summary | 12th Maths : UNIT 10 : Ordinary Differential Equations
Chapter: 12th Maths : UNIT 10 : Ordinary Differential Equations
Summary
SUMMARY
1. A
differential equation is any equation which contains at least one derivative of
an unknown function, either ordinary derivative or partial derivative.
2. The order of a differential equation is the
highest derivative present in the differential equation.
3. If a
differential equation is expressible in a polynomial form, then the integral
power of the highest order derivative appears is called the degree of the differential equation
4. If a
differential equation is not expressible to polynomial equation form having the
highest order derivative as the leading term then that the degree of the
differential equation is not defined.
5. If a
differential equation contains only ordinary derivatives of one or more
functions with respect to a single independent variable, it is said to be an
ordinary differential equation (ODE).
6. An
equation involving only partial derivatives of one or more functions of two or
more independent variables is called a partial differential equation (PDE).
7. The
result of eliminating one arbitrary constant yields a first order differential
equation and that of eliminating two arbitrary constants leads to a second
order differential equation and so on.
8. A
solution of a differential equation is an expression for the dependent variable
in terms of the independent variable(s) which satisfies the differential
equation.
9. The
solution which contains as many arbitrary constants as the order of the
differential equation is called the general
solution
10. If
we give particular values to the arbitrary constants in the general solution of
differential equation, the resulting solution is called a Particular Solution.
11. An
equation of the form f1 ( x)g1
( y)dx + f
2 ( x)g 2 ( y)dy = 0 is called an equation with variable
separable or simply a separable equation.
12. A
function f ( x, y) is said to be a homogeneous function of degree n in the variables x and y if, f (tx
, ty ) = t n
f ( x, y) for some n ∈ ℝ for all suitably restricted x , y
and t . This is known as Euler’s homogeneity.
13. If f ( x,
y) is a homogeneous function of
degree zero, then there exists a function g
such that f ( x, y) is always expressed in the form g(y/x).
14. An
ordinary differential equation is said to be in homogeneous form, if the
differential equation is written as dy/dx = g (y/x).
15. The
differential equation M ( x, y)dx + N(
x, y)dy =
0 [in differential form] is said to be homogeneous
if M and N are homogeneous functions of the same degree.
16. A first order differential equation of
the form
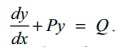
where P and Q are functions of x
only. Here no product of y and its
derivative dy/dx occurs and the dependent variable y and its derivative with respect to
independent variable x occur only in the first degree.
The
solution of the given differential equation (1) is given by ye∫Pdx = ∫ Qe∫Pdxdx + C .
Here e∫Pdx is known as the integrating factor
(I.F.)
17. A
first order differential equation of the form dx/dy + Px = Q , where P and Q are functions of y only. Here no product of x and its derivative dx/dy
occurs and the dependent variable x
and its derivative with respect to independent variable y occur only in the firstdegree.In this case, the solution is given
by xe∫
Pdy =
∫
Qe∫ Pdy dy + C
.
18. If x denotes the amount of the quantity
present at time t , then the
instantaneous rate at which the quantity changes at time t is dx/dt.
This
leads to a differential equation of the form dx/dt = f(x,t)
Related Topics