Ordinary Differential Equations

Ordinary Differential Equations

“Mathematics is the most beautiful and most powerful creation of the human spirit” - Stefan Banach

Introduction

Motivation and Early Developments

Just we look at some real life situations where

• the motion of projectile, rocket, satellite and planets

• the charge or current in the electric circuit

• the conduction of heat on a rod or in a slab

• the vibrations of a wire or membrane etc

are to be determined. The mathematical formulations of such problems emerge as differential equations under certain scientific laws. These laws involve various rates of change (derivatives) of one or more quantities with respect to other quantities. Thus the scientific laws manifest as mathematical equations involving derivatives, viz. differential equations.

Differential Equations emanate from the problems in geometry, mechanics, physics, chemistry, and engineering studies. We have studied about “rates” in our early classes. This is also known as instantaneous rate of change which is denoted as dy/dx.

We give below some relations between the rate of change and unknown functions that occur in real life situations.

(a) The rate of change of y with respect to x is directly proportional to y :

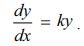
(b) The rate of change of y with respect to x is directly proportional to the product of y² and x :

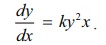
(c) The rate of change of y with respect to x is inversely proportional to y :

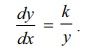
(d) The rate of change of y with respect to x is directly proportional to y² and inversely proportional to √x :

A differential equation is an equation in which some derivatives of the unknown function occur.

In many cases the independent variable is taken to be time.

In order to apply mathematical methods to a physical or “real life” problem, we must formulate the problem in mathematical terms; that is, we must construct a mathematical model for the problem. Many physical problems concern relationships between changing quantities. Since rates of change are represented mathematically by derivatives, mathematical models often involve equations relating to an unknown function and one or more of its derivatives. Such equations are differential equations. They are of basic significance in science and engineering since many physical laws as well as relations are modelled in the form of differential equations. Differential equations are much useful in describing mathematical models involving population growth or radio-active decay. The study of biological sciences and economics is incomplete without the application of differential equations.

The subject of differential equations was invented along with calculus by Newton and Leibniz in order to solve problems in geometry and physics. It played a crucial part in the development of Newtonian physics by the Bernoulli family, Euler, and others. Some of the applications of differential equations in our daily life are found in mobile phones, motor cars, air flights, weather forecast, internet, health care, or in many other daily activities.

In this chapter, we introduce and discuss the first order ordinary differential equations and some methods to find their solutions.

Learning Objectives

Upon completion of this chapter, students will be able to

• classify differential equations

• construct differential equations

• find the order and degree of the differential equations

• solve differential equation using the methods of variables separable, substitution, integrating factor

• apply differential equation in real life problems