Variables Separable Method

Solution of First Order and First Degree Differential Equations

Variables Separable Method

In solving differential equations, separation of variables was introduced initially by Leibniz and later it was formulated by John Bernoulli in the year 1694.

A first order differential equation is separable if it can be written as h ( y) y ′ = g( x) where the left side is a product of y′ and a function of y and the right side is a function of x . Rewriting a separable differential equation in this form is called the method of separation of variables.

Finding a solution to a first order differential equation will be simple if the variables in the equation can be separated. An equation of the form f₁ (x)g₁ ( y)dx + f ₂ (x)g ₂ ( y)dy = 0 is called an equation with variable separable or simply a separable equation.

Rewrite the given differential equation as

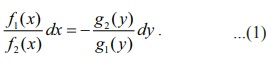
Integration of both sides of (1) yields the general solution of the given differential equation as 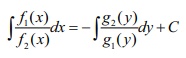 , where C is an arbitrary constant.

Remarks

1. No need to add arbitrary constants on both sides as the two arbitrary constants are combined together as a single arbitrary constant.

2. A solution with this arbitrary constant is the general solution of the differential equation.

“Solving a differential equation” is also referred to as “integrating a differential equation”, since the process of finding the solution to a differential equation involves integration.

Example 10.11

Example 10.12

Find the particular solution of (1+ x³ )dy − x² ydx = 0 satisfying the condition y(1) = 2

Solution

Given that (1+ x³ )dy − x²ydx = 0 .

The above equation is written as

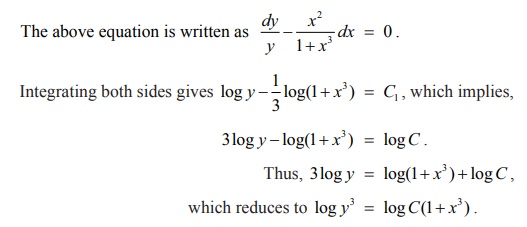
Hence, y ³ = C(1+ x³ ) gives the general solution of the given differential equation. It is given that when x = 1, y = 2. Then 2³ = C(1+1) ⇒ C = 4 and hence the particular solution is y³ = 4(1+ x³) .