Exercise 10.4: Solution of Ordinary Differential Equations

EXERCISE 10.4

1. Show that each of the following expressions is a solution of the corresponding given differential equation.

(i) y = 2x2 ; xy' = 2y

(ii) y = aex + be−x ; y′′ − y = 0

2. Find value of m so that the function y = emx is a solution of the given differential equation.

(i) y '+ 2 y = 0

(ii) y ''− 5 y' + 6y = 0

3. The slope of the tangent to the curve at any point is the reciprocal of four times the ordinate at that point. The curve passes through (2,5). Find the equation of the curve.

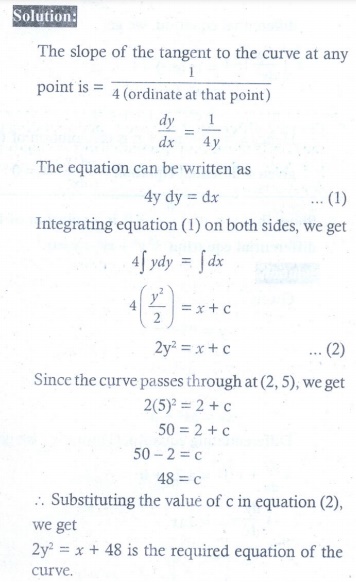
4. Show that y = e−x + mx + n is a solution of the differential equation  −1= 0.

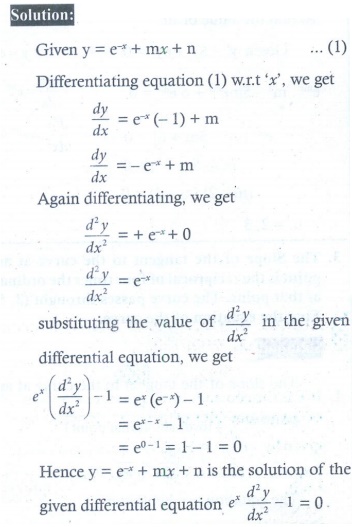
5. Show that y = ax + b/x , x ≠ 0 is a solution of the differential equation x2y′′ + xy′ − y = 0.

6. Show that y = ae−3x + b , where a and b are arbitrary constants, is a solution of the differential equation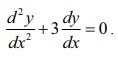 

7. Show that the differential equation representing the family of curves y2 = 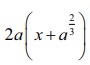, where a is a positive parameter, is .

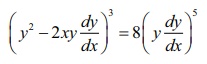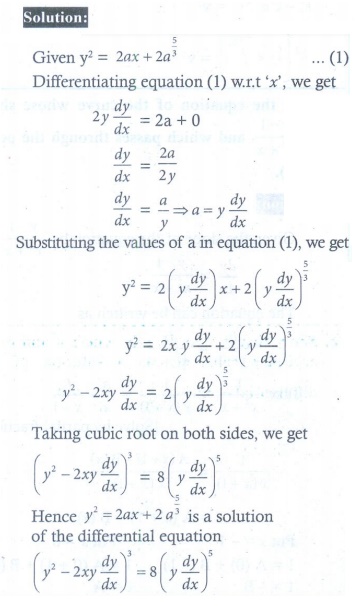
8. Show that y = a cos bx is a solution of the differential equation d2y/dx2 + b2y = 0.

Now, we discuss some standard methods of solving certain type of differential equations of the first order and first degree.

Answers:

2. (i) m = −2   (ii) m = 2, 3

3. 2y2 = x + 48