Differential Equation, Order, and Degree

Differential Equation, Order, and Degree

Definition 10.1

A differential equation is any equation which contains at least one derivative of an unknown function, either ordinary derivative or partial derivative.

For instance, let y = f ( x) where y is a dependent variable ( f is an unknown function) and x is an independent variable.

(1) The equation dy/dx = 0 is a differential equation.

(2) The equation dy/dx = sin x is a differential equation.

(3) The equation dy/dx + y = 7x + 5 is a differential equation.

(4) The equation d²y/dx² + dy/dx + y = sin x is a differential equation.

(5) The equation e^dy/dx = ln x, x > 0 is a differential equation.

(6) The equation 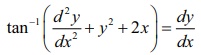 is a differential equation.

Definition 10.2 (Order of a differential equation)

The order of a differential equation is the highest order derivative present in the differential equation.

Thus, if the highest order derivative of the unknown function y in the equation is k^th derivative, then the order of the differential equation is k. Clearly k must be a positive integer.

For example, 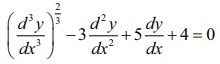 is a differential equation of order three.

Definition 10.3 (Degree of a differential equation)

If a differential equation is expressible in a polynomial form, then the integral power of the highest order derivative appears is called the degree of the differential equation

In other words, the degree of a differential equation is the power of the highest order derivative involved in the differential equation when the differential equation (after expressing in polynomial form) satisfies the following conditions :

(i) All of the derivatives in the equation are free from fractional powers, if any.

(ii) Highest order derivative should not be an argument of a transcendental function, trigonometric or exponential, etc. The coefficient of any term containing the highest order derivative should just be a function of x, y, or some lower order derivative but not as transcendental, trigonometric, exponential, logarithmic function of derivatives.

If one or more of the aforementioned conditions are not satisfied by the differential equation, it should be first reduced to the polynomial form in which it satisfies all of the above conditions.

If a differential equation is not expressible to polynomial equation form having the highest order derivative as the leading term then that the degree of the differential equation is not defined.

The determination of the degree of a given differential equation can be tricky if you are not well versed with the conditions under which the degree of the differential equation is defined. So go through the given solved examples carefully and master the technique of calculating the degree of the given differential equation just by sheer inspection!

Examples for the calculation of degree:

(1) Consider the differential equation 

The highest order derivative involved here is 2, and its power is 1 in the equation. Thus, the order of the differential equation is 2 and degree is 1.

(2) Consider the differential equation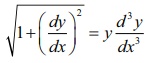 

Since this equation involves fractional powers, we must first get rid of them. On squaring the equation, we get

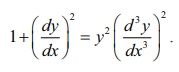
Now, we can clearly make out that the highest order derivative is 3. Therefore order of the differential equation is 3 and since its power is 2 in the equation, the degree of the differential equation is 2.

(3) Consider the differential equation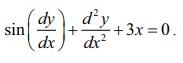 

Here, the highest order derivative is 2. Because of sine of first derivative, the given differential equation can not be expressed as polynominal equation. So, the order of the differential equation is 2, and, it is not in polynomial equation in derivatives and so degree is not defined.

(4) Consider the equation 

Here, the highest order derivative (order is 2) has involvement in an exponential function. This cannot be expressed as polynomial equation with d²y / dx² as the leading term So, the degree of the equation is not defined. The order of the equation is 2.

(5) Further, the following differential equations do not have degrees.

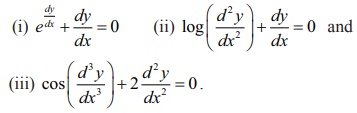
(6) The differential equation 10(y′′′)⁴ + 7 ( y′′)⁵ + sin( y′) + 5 = 0 has order 3 but degree is not defined.

(7) The differential equation cos( y′) y′′′ + 5 y ′′ + 7 y′ = sin x has order 3 and degree is not defined.

Remark

Observe that the degree of a differential equation is always a positive integer.

Example 10.1

Determine the order and degree (if exists) of the following differential equations:

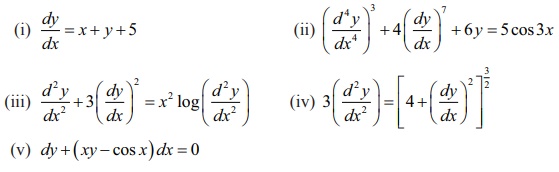
Solution

(i) In this equation, the highest order derivative is dy/dx whose power is 1 Therefore, the given differential equation is of order 1 and degree 1.

(ii) Here, the highest order derivative is d⁴y/ dx² whose power is 3.

Therefore, the given differential equation is of order 4 and degree 3.

(iii) In the given differential equation, the highest order derivative is d²y/dx² whose power is 1.

Therefore, the given differential equation is of order 2.

The given differential equation is not a polynomial equation in its derivatives and so its degree is not defined.

(iv) The given differential equation is

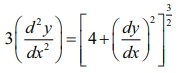
Squaring both sides, we get

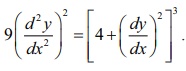
In this equation, the highest order derivative is d²y/ dx² whose power is 2.

Therefore, the given differential equation is of order 2 and degree 2.

(v) dy + ( xy − cos x ) dx = 0 is a first order differential equation with degree 1, since the equation can be rewritten as dy/dx + xy − cos x = 0 .