Solution of Ordinary Differential Equations

Solution of Ordinary Differential Equations

Definition 10.9 : (Solution of DE)

A solution of a differential equation is an expression for the dependent variable in terms of the independent variable(s) which satisfies the differential equation.

Caution

(i) There is no guarantee that a differential equation has a solution.

For instance, ( y '(x))² + y² +1 = 0 has no solution, since ( y '( x))² = − ( y² +1) and so y '(x) cannot be real.

(ii) Also, a solution of a differential equation, if exists, is not unique.

For instance, the functions y = e^2x , y = 2e^2x , y = √8e^2x are solutions of same equation dy/dx − 2 y = 0. In fact, y = ce^2x , c ∈ ℝ, are all solutions of the differential equation dy/dx − 2y = 0.

Thus, to represent all possible solutions of a differential equation, we introduce the notion of the general solution of a differential equation.

Definition 10.10 : (General solution)

The solution which contains as many arbitrary constants as the order of the differential equation is called the general solution

Remark

The general solution includes all possible solutions and typically includes arbitrary constants (in the case of an ODE) or arbitrary functions (in the case of a PDE.)

Definition 10.11 : (Particular solution)

If we give particular values to the arbitrary constants in the general solution of differential equation, the resulting solution is called a Particular Solution.

Remark

(i) Often we find a particular solution to a differential equation by giving extra conditions.

(ii) The general solution of a first order differential equation y ' = f ( x , y) represents a one parameter family of curves in xy -plane.

For instance, y = ce^2x , c ∈ ℝ, is the general solution of the differential equation dy/dx − 2y = 0.

For instance, we have already seen that y = a cos x + b sin x satisfies the second order differential equation d²y/dx² + y = 0 . Since it contains two arbitrary constants, it is the general solution of d²y/dx² + y = 0 . If we put a = 1, b = 0 in the general solution, then we get y = cos x is a particular solution of the differential equation d²y/dx² + y = 0.

In application, differential equations do not arise by eliminating the arbitrary constants. They frequently arise while investigating many physical problems in all fields of engineering, science and even in social sciences. Mostly these differential equations are also accompanied by certain conditions on the variables to obtain unique solution satisfying the given conditions.

Example 10.7

Show that x² + y² = r² , where r is a constant, is a solution of the differential equation dy/dx  = − x/ y.

Solution

Given that x² + y² = r² , r ∈ ℝ                       ... (1)

The given equation contains exactly one arbitrary constant.

So, we have to differentiate the given equation once. Differentiate (1) with respect to x , we get

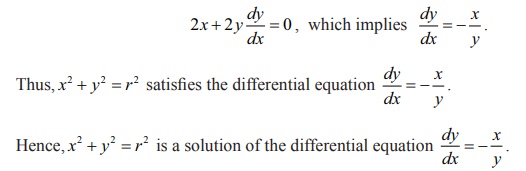
Thus, x² + y² = r² satisfies the differential equation dy/dx = − x/y.

Hence, x² + y² = r² is a solution of the differential equation dy/dx = − x/y.

Example 10.8

Show that y = mx + 7/m, m ≠ 0 is a solution of the differential equation xy'+ 7(1/y') – y  = 0. 

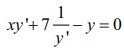
Solution

The given function is y = mx + 7/m, where m is an arbitrary constant. ... (1)

Differentiating both sides of equation (1) with respect to x , we get y ' = m .

Substituting the values of y ' and y in the given differential equation,

we get xy′ + 7/y′ − y = xm + 7/m − mx – 7/m = 0 .

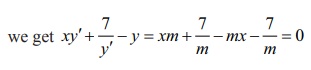
Therefore, the given function is a solution of the differential equation xy'+ 7(1/y’) − y = 0. 

Example 10.9

Show that y = 2(x² – 1) + Ce^{− x2} is a solution of the differential equation dy/dx + 2xy − 4x³ = 0 . 

Solution

The given function is y = 2 ( x² −1) + Ce^{− x2} , where C is an arbitrary constant.  ...(1)

Differentiating both sides of equation (1) with respect to x , we get dy/dx = 4x − 2xCe^{− x2} . 

Substituting the values of dy/dx and y in the given differential equation, we get

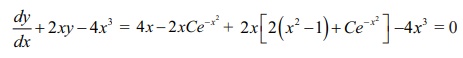
Therefore, the given function is a solution of the differential equation dy/dx + 2xy − 4x³ = 0 .

Example 10.10

Show that y = a cos(log x ) + b sin ( log x ) , x > 0 is a solution of the differential equation x² y′′ + xy′ + y = 0 .

Solution

The given function is y = a cos(log x ) + b sin ( log x)                ...(1)

where a, b are two arbitrary constants. In order to eliminate the two arbitrary constants, we have to differentiate the given function two times successively.

Differentiating equation (1) with respect to x , we get

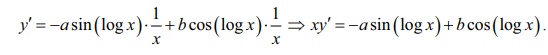
Again differentiating this with respect to x, we get

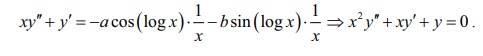
Therefore, y = a cos(log x ) + b sin ( log x) is a solution of the given differential equation.