Solution of First Order and First Degree Differential Equations | Mathematics - Substitution Method | 12th Maths : UNIT 10 : Ordinary Differential Equations
Chapter: 12th Maths : UNIT 10 : Ordinary Differential Equations
Substitution Method
Solution of First Order and First Degree Differential Equations
Substitution
Method
Let the
differential equation be of the form dy/dx
=
f (ax + by
+
c).
(i) If a ≠ 0 and b ≠ 0 , then the substitution ax
+
by + c
=
z reduces the given equation to the variables
separable form.
(ii) If a = 0 or b = 0 , then the differential equation is already in separable
form.


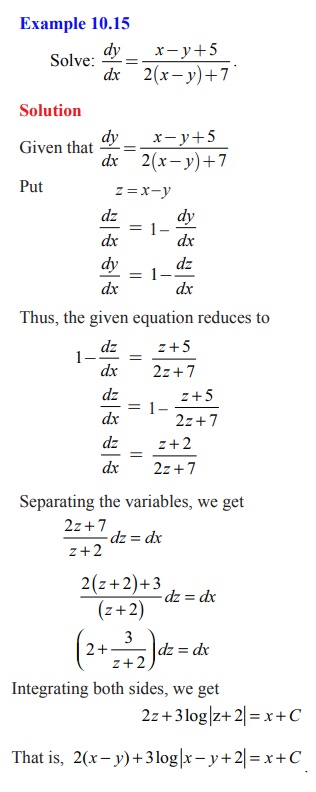
Example 10.16
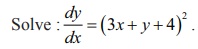
Solution
To solve the given differential equation, we make the substitution
3x + y + 4 = z.
Differentiating with respect to x, we get dy/dx = dz/dx
− 3 . So the given differential equation becomes 
In this equation variables are separable. So, separating the
variables and integrating, we get the general solution of the given
differential equation as
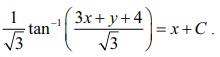
Related Topics