Exercise 10.8: Applications of First Order Ordinary Differential Equations

EXERCISE 10.8

1. The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours, find how many bacteria will be present after 10 hours?

2. Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years the population increased from 3,00,000 to 4,00,000.

3. The equation of electromotive force for an electric circuit containing resistance and self-inductance is E = Ri + L dt/di , where E is the electromotive force is given to the circuit, ℝ the resistance and L, the coefficient of induction. Find the current i at time t when E = 0.

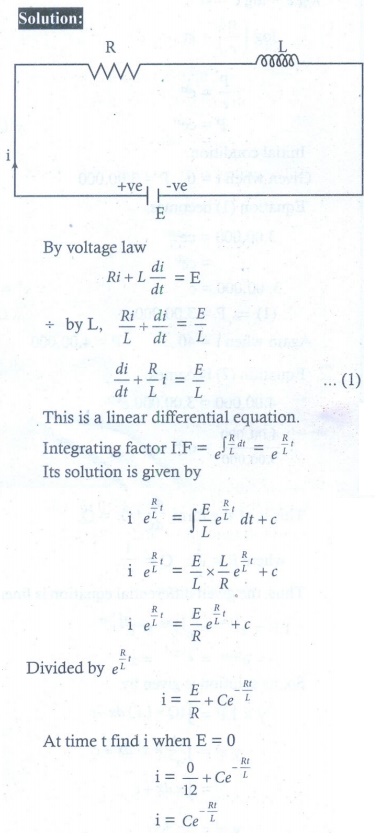
4. The engine of a motor boat moving at 10 m / s is shut off. Given that the retardation at any subsequent time (after shutting off the engine) equal to the velocity at that time. Find the velocity after 2 seconds of switching off the engine.

5. Suppose a person deposits ₹10,000 in a bank account at the rate of 5% per annum compounded continuously. How much money will be in his bank account 18 months later?

6. Assume that the rate at which radioactive nuclei decay is proportional to the number of such nuclei that are present in a given sample. In a certain sample 10% of the original number of radioactive nuclei have undergone disintegration in a period of 100 years. What percentage of the original radioactive nuclei will remain after 1000 years?

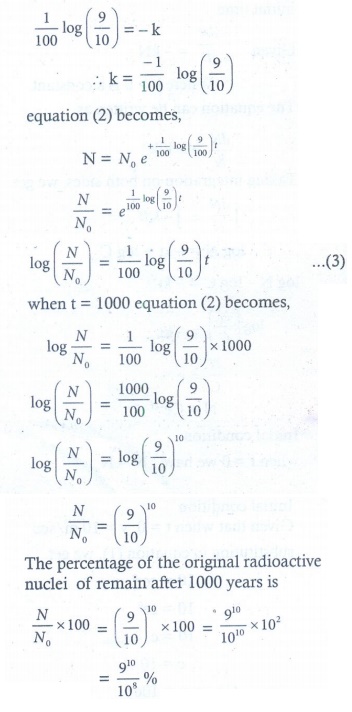
7. Water at temperature 100 º C cools in 10 minutes to 80º C in a room temperature of 25º C . Find

(i) The temperature of water after 20 minutes

(ii) The time when the temperature is 40º C

[ loge (11/15) = −0.3101; loge 5 = 1.6094 ]

8. At 10.00 A.M. a woman took a cup of hot instant coffee from her microwave oven and placed it on a nearby Kitchen counter to cool. At this instant the temperature of the coffee was 180º F, and 10 minutes later it was 160º F . Assume that constant temperature of the kitchen was 70 º F .

(i) What was the temperature of the coffee at 10.15A.M.?  [ log(9/11) = −0.6061]

(ii) The woman likes to drink coffee when its temperature is between 130 º F and 140 º F between what times should she have drunk the coffee? [log (6/11) = - 0.2006]

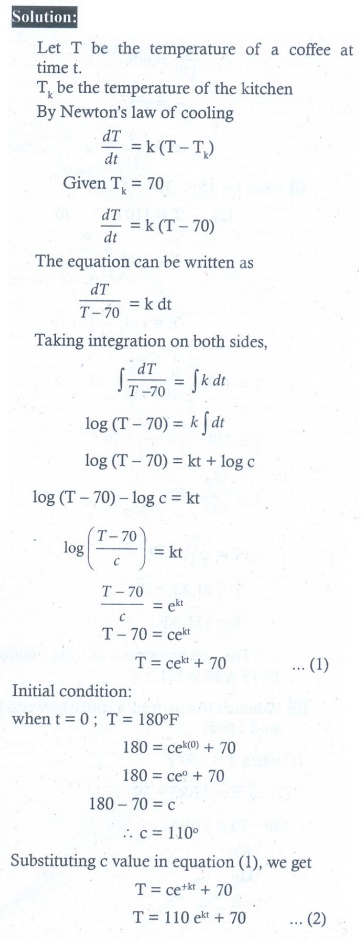
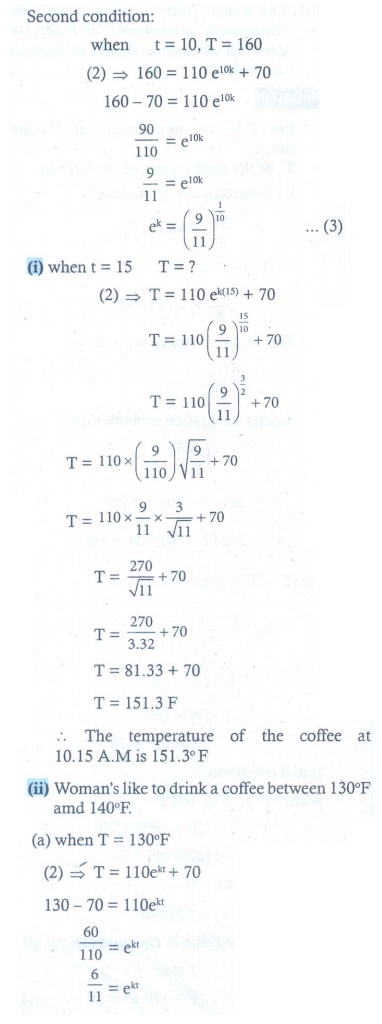
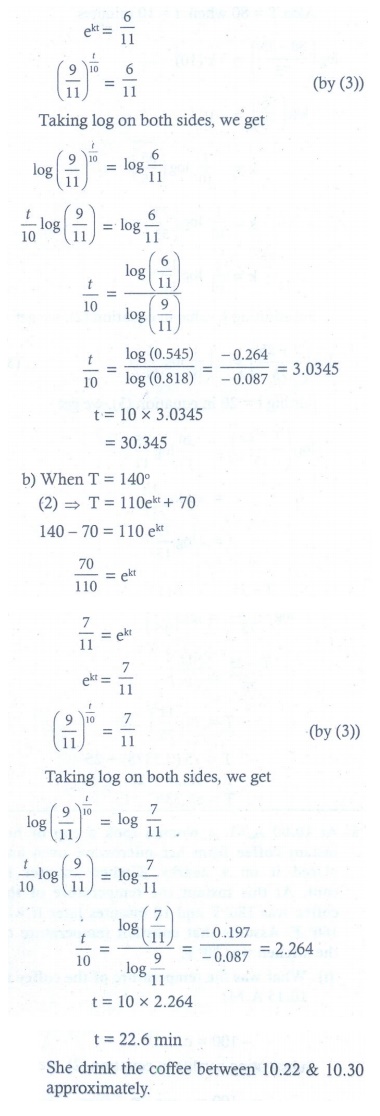
9. A pot of boiling water at 100 º C is removed from a stove at time t = 0 and left to cool in the kitchen. After 5 minutes, the water temperature has decreased to 80 º C , and another 5 minutes later it has dropped to 65 º C . Determine the temperature of the kitchen.

10. A tank initially contains 50 litres of pure water. Starting at time t = 0 a brine containing with 2 grams of dissolved salt per litre flows into the tank at the rate of 3 litres per minute. The mixture is kept uniform by stirring and the well-stirred mixture simultaneously flows out of the tank at the same rate. Find the amount of salt present in the tank at any time t > 0 .

Answers:

1. After 10 hours the number of bacteria as 9 times the original number of bacteria.

2. P = 300000 (4/3)t/40

3. i = Ce – Rt/L

4. v = 10/e2

5. P = 10000e0.075

6.  910/108   % of the radioactive element will remain after 1000 years.

7. (i) 65.33ºC (ii) 51.91 mts

8. (i) T  ≈ 151ºF  (ii) t = 22.523. She drunk the coffee between 10.22 and 10.30 approximately.

9. 20º

10. x = 100 ( 1− e − 3t/50)