Formation of Differential Equations from Geometrical Problems

Formation of Differential Equations from Geometrical Problems

Given a family of functions parameterized by some constants, a differential equation can be formed by eliminating those constants of this family. For instance, the elimination of constants A and B from y = Ae^x + B e^{− x} , yields a differential equation d²y/dx² − y = 0.

Consider an equation of a family of curves, which contains n arbitrary constants. To form a differential equation not containing any of these constants, let us proceed as follows:

Differentiate the given equation successively n times, getting n differential equations. Then eliminate n arbitrary constants from (n +1) equations made up of the given equation and n newly obtained equations arising from n successive differentiations. The result of elimination gives the required differential equation which must contain a derivative of the nth order.

Example 10.2

Find the differential equation for the family of all straight lines passing through the origin.

Solution

The family of straight lines passing through the origin is y = mx , where m is an arbitrary constant.                  … (1)

Differentiating both sides with respect to x, we get

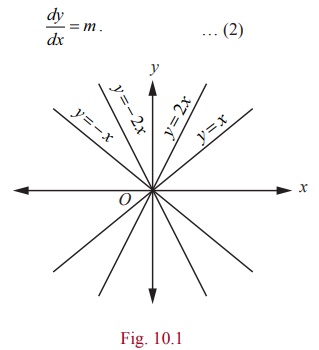
From (1) and (2), we get y = x dy/dx. This is the required differential equation.

Observe that the given equation y = mx contains only one arbitrary constant and thus we get the differential equation of order one.

Example 10.3

Form the differential equation by eliminating the arbitrary constants A and B from y = A cos x + Bsin x .

Solution

Given that

  y = A cos x + Bsin x             ... (1)

Differentiating (1) twice successively, we get

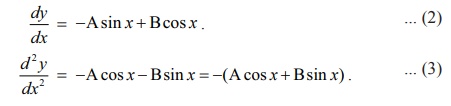
Substituting (1) in (3), we get d²y/dx² + y = 0 as the required differential equation.

Example 10.4

Find the differential equation of the family of circles passing through the points ( a, 0) and ( −a, 0) .

Solution

A circle passing through the points ( a, 0) and ( −a, 0) has its centre on y - axis.

Let ( 0, b) be the centre of the circle. So, the radius of the circle is √[a² + b²].

Therefore the equation of the family of circles passing through the points ( a, 0) and ( −a, 0) is x² + ( y − b)² = a² + b² , b is an arbitrary constant.

Differentiating both sides of (1) with respect to x, we get

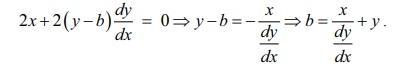
Substituting the value of b in equation (1), we get

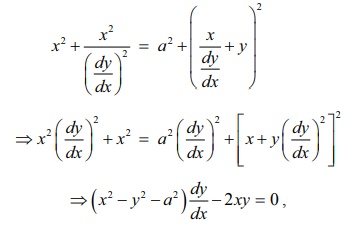
 ⇒ ( x² − y² − a² ) dy/dx − 2xy = 0 , which is the required differential equation.

Example 10.5

Find the differential equation of the family of parabolas y² = 4ax , where a is an arbitrary constant.

Solution

The equation of the family of parabolas is given by y² = 4ax , a is an arbitrary constant. ... (1)

Differentiating both sides of (1) with respect to x , we get 2y dy/dx = 4 a ⇒ a = y/2 dy/dx

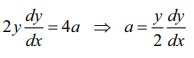
Substituting the value of a in (1) and simplifying, we get dy/dx = y/2x as the required differential equation.

Example 10.6

Find the differential equation of the family of all ellipses having foci on the x -axis and centre at the origin.

Solution

The equation of the family of all ellipses having foci on the x -axis and centre at the origin is given by

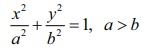
where a and b are arbitrary constants.

Differentiating equation (1) with respect to x, we get

Substituting the value of 1/a² in equation (2) and simplifying, we get

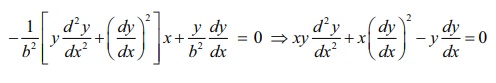
which is the required differential equation.

Remark

The result of eliminating one arbitrary constant yields a first order differential equation and that of eliminating two arbitrary constants leads to a second order differential equation and so on.