Homogeneous Form or Homogeneous Differential Equation

Homogeneous Form or Homogeneous Differential Equation

Definition 10.12 : (Homogeneous Function of degree n)

A function f ( x, y) is said to be a homogeneous function of degree n in the variables x and y if, f (tx , ty ) = t ⁿ f ( x, y) for some n ∈ ℝ for all suitably restricted x , y and t . This is known as Euler’s homogeneity.

For instance,

(i) f (x, y) = 6x² + 2xy + 4 y² is a homogeneous function in x and y, of degree two.

(ii) But f (x, y) = x³ + ( sin x)e^y is not a homogeneous function.

If f ( x, y) is a homogeneous function of degree zero, then there exists a function g such that f ( x, y) is always expressed in the form g(y/x) or g(x/y).

Definition 10.13: (Homogeneous Differential Equation)

An ordinary differential equation is said to be in homogeneous form, if the differential equation is written as dy/dx = g(y/x) .

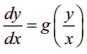
Caution

The word “homogeneous” used in Definition 10.7 is different from in Definition 10.12.

Remark

(i) The differential equation M ( x, y)dx + N( x, y)dy = 0 [in differential form] is said to be homogeneous if M and N are homogeneous functions of the same degree.

(ii) The above equation is also written as dy/dx = f ( x, y) [in derivative form] where

f ( x, y) = −M ( x, y) / N ( x, y) is clearly homogeneous of degree 0 .

For instance

(1) consider the differential equation (x² − 3y²)dx + 2xy dy = 0 . The given equation is rewritten as 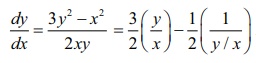. Thus, the given equation is expressed as  Hence, (x² - 3y²)dx + 2xydy = 0 is a homogeneous is a homogeneous is a homogeneous differential equation.

(2) However, the differential equation 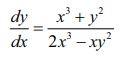 is not homogeneous. (verify!)

To find the solution of a homogeneous differential equation dy/dx = g(y/x), consider the substitution v = y/x. Then, y = xv and dy/dx = v + x dv/dx .Thus, the given differential equation becomes x dv/dx = f (v) − v which is solved using variables separable method. This leads to the following result.

Theorem 10.1

If M ( x, y ) dx + N( x , y)dy = 0 is a homogeneous equation, then the change of variable y = vx, transforms into a separable equation in the variables v and x .