First Order Linear Differential Equations

First Order Linear Differential Equations

A first order differential equation of the form

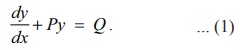
where P and Q are functions of x only. Here no product of dy/dx and its derivative dy/dx occur and the dependent variable y and its derivative with respect to independent variable x occurs only in the first degree.

To integrate (1), let us consider the homogeneous equation dy/dx + Py = 0 . ….(2)

The equation (2) can be integrated as follows:

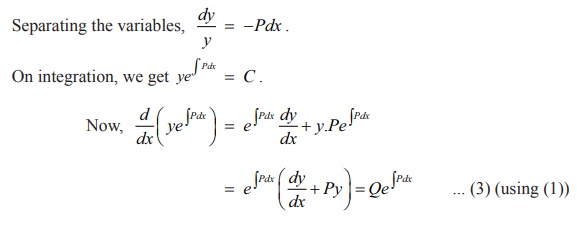
Integrating both sides of (3) with respect to x, we get the solution of the given differential equation as

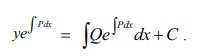
Here e^∫Pdx is known as the integrating factor (I.F.) of (1).

Remarks

1. The solution of linear differential equation is

 y × (I.F ) = ∫Q(I .F )dx + C , where C is an arbitrary constant.

2. In the integrating factor e^{∫ Pdx} , P is the coefficient of y in the differential equation provided the coefficient of dy/dx is unity.

3. A first order differential equation of the form dx/dy + Px = Q , where P and Q are functions of y only. Here no product of x and its derivative dx/dy occur and the dependent variable x and its derivative with respect to independent variable y occurs only in the first degree.

In this case, the solution is given by xe^{∫ Pdy} = ∫Qe^{∫ Pdy} dy + C .