Classification of Differential Equations

Classification of Differential Equations

Definition 10.4: (Ordinary Differential Equation)

If a differential equation contains only ordinary derivatives of one or more functions with respect to a single independent variable, it is said to be an Ordinary Differential Equation (ODE).

Definition 10.5: (Partial Differential Equation)

An equation involving only partial derivatives of one or more functions of two or more independent variables is called a Partial Differential Equation (PDE).

For instance, let y denote the unknown function and x be independent variable. Then

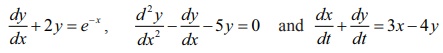
are some examples of ordinary differential equations.

For instance,

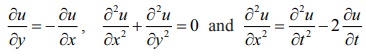
are some examples of partial differential equations.

In this chapter, we discuss ordinary differential equations only.

Ordinary differential equations are classified into two different categories namely linear ordinary differential equations and nonlinear ordinary differential equations.

Definition 10.6

A general linear ordinary differential equation of order n is any differential equation that can be written in the following form.

a_n ( x) y^{( n)} + a_n−1 ( x) y^{( n−1)} + . . .  + a₁ ( x) y' + a₀ y = g ( x)         ... (1)

where the coefficients a_n ( x ) ≠ 0, a₀ ( x ) , a₁ ( x ), . . . , a_n−1 ( x ) and g ( x) are any function of independent variable x (including the zero function)

Note

(1) The important thing to note about linear differential equations is that there are no products of the function, y ( x) , and its derivatives and neither the function nor its derivatives occur to any power other than the first power.

(2) No transcendental functions – (trigonometric or logarithmic etc) of y or any of its

derivatives occur in differential equation.

(3) Also note that neither the function nor its derivatives are “inside” another function, for instance, √y′ or e^y′.

(4) The coefficients a₀ ( x ) , a₁ ( x ), . . . , a_n−1 ( x ) and g( x) can be zero or non-zero functions, or constant or non-constant functions, linear or non-linear functions. Only the function, y (x) , and its derivatives are used in determining whether a differential equation is linear.

Definition 10.7

A nonlinear ordinary differential equation is simply one that is not linear.

If the coefficients of y , y′, y ′′, , y( ⁿ) contain the dependent variable y or its derivatives or if powers of y , y′, y ′′, , y(ⁿ) , such as (y′)² , appear in the equation, then the differential equation is nonlinear. Also, nonlinear functions of the dependent variable or its derivatives, such as sin y or e^y′ cannot appear in a linear equation.

For instance,

(1) dy/dx = ax³ , d²y//dx² + 2dy/dx + y = 0 and dy/dx + p(x) y = q(x) are linear differential equations where as y dy/dx + sin x = 0 is a nonlinear differential equation.

(2) y ′′ + 2x³y ′ = 7xy + x² is a second order linear ODE.

(3) y ′′ + y′ = √x is a second order linear ODE.

(4) y ² + y′ = √x is a first order nonlinear ODE.

(5) y ′ = x sin( y) is a first order nonlinear ODE.

(6) y ′′ = y sin( x) is a second order linear ODE.

Definition 10.8

If g ( x) = 0 in (1), then the above equation is said to be homogeneous, otherwise it is called non-homogeneous.

Remark

If y_i(x), i = 1, 2 are any two solutions of homogeneous equation

 a_n (x) y ⁽ⁿ⁾ (x) + a_{n −1} (x) y ⁽ⁿ⁻¹⁾ (x) +. . . + a₁ (x) y '(x) + a₀ (x) y ( x) = 0       …(2)

then a_n (x) y_i^{( n)} (x) + a_{n −1} (x) y_i^{( n−1)} (x) + . . . + a₁ (x) y_i (x) + a₀ (x) y_i (x) = 0, i = 1, 2 .

Suppose u ( x) = c₁ y₁ (x ) + c₂ y ₂ (x) , where c₁ and c₂ are arbitrary constants. Then, it can be easily verified that u ( x) is also a solution of (2).

Thus, a first order linear differential equation is written as y′ + p( x ) y = f ( x) . A first order differential equation that can’t be written like this is nonlinear. Since y = 0 is obviously a solution of the homogeneous equation y′ + p(x ) y = 0 , we call it the trivial solution. Any other solution is nontrivial. In fact this is true for a general linear homogeneous differential equation as well.