Applications of First Order Ordinary Differential Equations

Applications of First Order Ordinary Differential Equations

The subject of differential equations has vast applications in solving real world problems. The solutions of the differential equations are used to predict the behaviors of the system at a future time, or at an unknown location. In several problems, the rate at which a quantity changes is a given function of the quantity and /or the time. The objective is to find the quantity itself. If x denotes the amount of the quantity present at time t , then the instantaneous rate at which the quantity changes at time t is dx/dt . This leads to a differential equation of the form dx/dt = f ( x, t) . In this section we shall consider this type of problems only. Further, by rate, we mean the instantaneous rate only.

1. Population growth

Now, we consider the growth of a population (for example, human, an animal, or a bacteria colony) as a function of time t .

Let x(t) be the size of the population at any time t . Although x(t) is integer-valued, we approximate x(t) as a differentiable function and techniques of differential equation can be applied to determine x(t) . Assume that population grows at a rate directly proportional to the amount of population present at that time. Then, we obtain

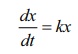
dx/dt = kx , where k is the constant of proportionality .               … (1)

Here k > 0 , since the population always increases.

The solution of the differential equation is x(t) = Ce^kt , where C is a constant of integration. The values of C and k are determined with the help of initial conditions. Thus, the population increases exponentially with time. This law of population growth is called Malthusian law.

Example 10.27

The growth of a population is proportional to the number present. If the population of a colony doubles in 50 years, in how many years will the population become triple?

Solution

Let x(t) be the population at time t . Then dx/dt = kx .

By separating the variables, we obtain dx/x = kdt .

Integrating on both sides, we get, log |x| = kt + log |C| or x = Ce^kt , where C is an arbitrary constant.

Let x₀ be the population when t = 0 and obtain C = x₀ .

Thus, we get x = x₀e^kt .

Now x = 2x₀ , when t = 50 and thus, k = 1/50 log 2 .

Hence, x = x₀ 2^t/50 is the population at any time t.

Assume that the population is tripled in t₁ years.

That is, x = 3x₀ , when t = t₁ .

Thus, t1 = 50 (log3/ log2).Therefore, the population is tripled in 50(log3/ log2) years. 

2. Radioactive decay

The nucleus of an atom consists of combinations of protons and neutrons. Many of these combinations of protons and neutrons are unstable, that is the atoms decay or transmute into the atoms of another substance. Such nuclei are said to be radioactive.

It is assumed that the rate dA/dt at which the nuclei of a substance decays is proportional to the  amount A(t) of the substance remaining at time t.

Thus, the required differential equation is

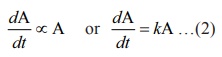
dA/dt ∝ A or dA/dt = kA …(2),

where k is the constant of proportionality. Here k < 0 , since decay occurs.

Remarks

From equations (1) and (2), we see that the differential equations are the same, but the difference is only in the interpretations of the symbols and the constants of proportionality. For growth as we expect in (1), k > 0 and in the case of (2) for decay, k < 0 .

A single differential equation can serve as a mathematical model for many different phenomena.

Example 10.28

A radioactive isotope has an initial mass 200mg , which two years later is 50mg . Find the expression for the amount of the isotope remaining at any time. What is its half-life? (half-life means the time taken for the radioactivity of a specified isotope to fall to half its original value).

Solution

Let A be the mass of the isotope remaining after t years, and let −k be the constant of proportionality, where k > 0 . Then the rate of decomposition is modeled by dA/dt = −kA , where the minus sign indicates that the mass is decreasing. It is a separable equation. Separating the variables, we get dA / A = −kdt

Integrating on both sides, we get log |A| = −kt + log |C| or A = Ce^−kt .

Given that the initial mass is 200mg. That is, A = 200 when t = 0 and thus, C = 200 .

Thus, we get A = 200e^−kt .

Also, A = 150 when t = 2 and therefore, k = 1/2 log (4/3).

Hence, 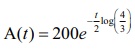 is the mass of isotope remaining after t years.

The half-life t_h is the time corresponding to A = 100mg .

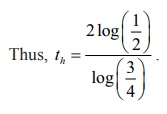
3. Newton’s Law of cooling/warming

Consider pouring a 150° cup of coffee and kept it on the table in an 80°C room.

What happens to the temperature of the coffee? We observe that the cup of coffee will cool off until it reaches the room temperature.

Now consider taking a 35° glass of cold water from the refrigerator and kept it on the table in an 80°C room. What happens to the temperature of the cold water? Similarly, we can observe the water will warm up until it reaches room temperature.

According to Newton’s law of cooling or warming, the rate at which the temperature of a body changes is proportional to the difference between the temperature of the body and the temperature of the surrounding medium the so-called ambient temperature. If T (t) represents the temperature of a body at time t , T_m the temperature of the surrounding medium, and dT/dt the rate at which the temperature of the body changes, then Newton’s law of cooling(or warming) is dT/dt ∝ T −T_m or dT/dt = k ( T − T_m ) , where k is constant of proportionality. In either case, cooling or warming, if T_m is constant, it stands to reason that k < 0 .

Example 10.29

In a murder investigation, a corpse was found by a detective at exactly 8 p.m. Being alert, the detective also measured the body temperature and found it to be 70^oF. Two hours later, the detective measured the body temperature again and found it to be 60^oF. If the room temperature is 50^oF, and assuming that the body temperature of the person before death was 98.6^oF, at what time did the murder occur?

[log ( 2.43 ) = 0.88789; log ( 0.5 ) = −0.69315 ]

Solution

Let T be the temperature of the body at any time t and with time 0 taken to be 8 p.m.

By Newton’s law of cooling,

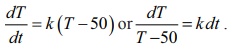
Integrating on both sides, we get log |50 – T| = kt + log C or 50 − T = Ce^kt .

When t = 0, T = 70 , and so C = −20

When t = 2,T = 60 , we have −10 = −20e^k2.

Thus, k = 1/2 log(1/2) .

Hence, the solution is 50 − T = 

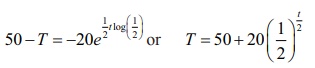
Now, we would like to find the value of t, for which T (t) = 98.6 , and

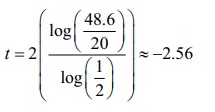
It appears that the person was murdered at about 5.30 p.m.

4. Mixture problems

Mixing problems occur quite frequently in chemical industry. Now we explain how to solve the basic model involving a single tank.

A substance S is allowed to flow into a certain mixture in a container at a constant rate, and the mixture is kept uniform by stirring. Further, in one such situation, this uniform mixture simultaneously flows out of the container at another rate. Now we seek to determine the quantity of the substance S present in the mixture at time t .

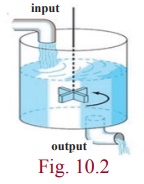
Letting x to denote the amount of S present at time t and the derivative dx/dt to denote the rate of change of x with respect to t . If IN denotes the rate at which S enters the mixture and OUT denotes the rate at which it leaves, then we have the equation dx/dt = IN – OUT

Example 10.30

A tank contains 1000 litres of water in which 100 grams of salt is dissolved. Brine (Brine is a high-concentration solution of salt (usually sodium chloride) in water) runs in a rate of 10 litres per minute, and each litre contains 5grams of dissolved salt. The mixture of the tank is kept uniform by stirring. Brine runs out at 10 litres per minute. Find the amount of salt at any time t .

Solution

Let x(t) denote the amount of salt in the tank at time t . Its rate of change is dx/dt = in flow rate - out flow rate

Now, 5 grams times 10 litres gives an inflow of 50 grams of salt. Also, the out flow of brine is 10 litres per minute. This is 10 / 1000 = 0.01 of the total brine content in the tank. Hence, the outflow of salt is 0.01 times x(t) , that is 0.01x(t) .

Thus the differential equation for the model is dx/dt = 50 − 0.01x = −0.01( x − 5000)

This can be written as

dx / x–5000 = −(0.01)dt

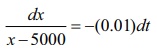
Integrating both sides, we obtain log | x – 5000 | = −0.01t + log C

or x − 5000 = Ce^−0.01t or x = 5000 + Ce^−0.01t

Initially, when t = 0, x = 100 , so 100 = 5000 + C .Thus, C = −4900 .

Hence, the amount of the salt in the tank at time t is x = 5000 − 4900e^−0.01t .