Chapter: 11th 12th std standard Class Organic Inorganic Physical Chemistry Higher secondary school College Notes
Shapes of orbitals: s, p, d Shapes
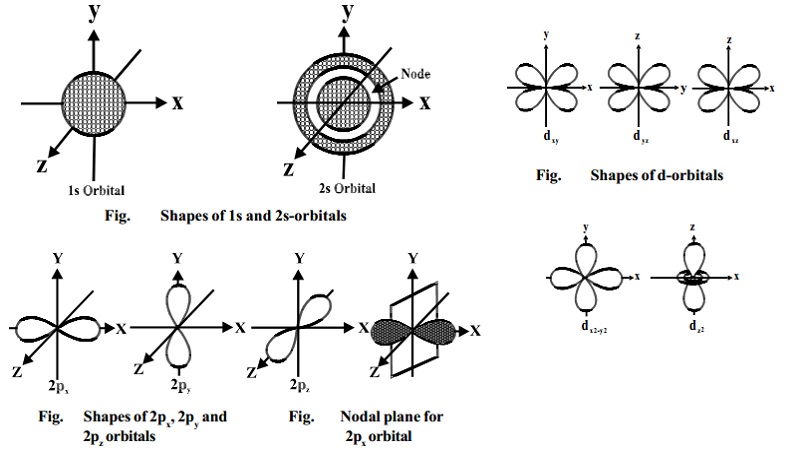
Shapes of orbitals
An orbital is the region of space around the nucleus within which the
probability of finding an electron of given energy is maximum .The shape of
this region (electron cloud) gives the shape of the orbital. The plot of
angular wave functions or square of angular wave functions (probability
functions) give us the shapes of orbitals.These two plots differ only slightly.
Let us consider the individual shapes.
Shape of s-orbitals
For s-orbitals, when l = 0,
the value of m is 0 i.e., there is only one possible orientation. This means
that the probability of finding an electron is the same in all directions at a
given distance from the nucleus. It should, therefore, be spherical in shape.
Hence all s- orbitals are non- directional and spherically symmetrical about
the nucleus.
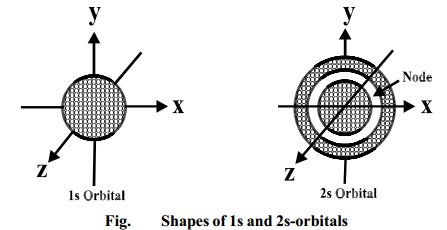
The size
of an s-orbital depends upon value of the principal quantum number n. Greater
the value of 'n' larger is the size of the orbital.
An important feature of the 2s-orbital is that there is a spherical
shell within this orbital where the probability of finding the electron is zero
(nearly). This is called a node or nodal surface. In 2s orbital there is one
spherical node. The number of nodal surfaces or nodes in s-orbital of any
energy level is equal to (n-1), where n is the principal quantum number.
Shape of p-orbitals
For p-subshell l = 1, there
are three values of m namely -1, 0, +1. It means that p orbitals can have three
possible orientations. These three p-orbitals are equal in energy (degenerate
state) but differ in their orientations. Each p-orbital consists of two lobes
symmetrical about a particular axis. Depending upon the orientation of the
lobes, these are denoted as 2px , 2py and 2pz
accordingly as they are symmetrical about X,Y and Z - axis respectively.

The lines
in the figure represents the cross-section of the three dimensional boundary
surface of p-orbitals. The boundary surface means the surface which encloses 90
percent of the dots representing the electrons. Two lobes of each p-orbital are
separated by a nodal plane (a plane having zero electron density). For example,
for 2px orbital, YZ plane is the nodal plane x
Thus, p-orbitals have dumb-bell shape and have directional character.
The probability of finding the electron is equal in both the lobes. The
p-orbitals of higher energy levels have similar shapes although their size are
bigger.
Shape of d-orbitals
For
d-subshell, l = 2, there are five
values of m namely -2, -1, 0, 1, 2. It
means d-
orbitals can have five orientations. These are represented by dxy, dyz,

dzx, dx2-y2 and dz2; for
example, 3dxy, 3dyz, 3dzx, 3dx2-y2
and 3dz2. The dxy, dyz and dzx
orbitals have same shape i.e., clover leaf shape but they lie in XY, YZ and ZX-
planes respectively.The dz2 orbital is symmetrical about
Z-axis and has a dumb - bell shape with a doughnut shaped electron cloud in the
centre. The dx2-y2 orbital is also clovar leaf shaped but its leaves
are directed along the X and Y- axis.
The reason
for the presence of four lobes in any nd orbital lies in the fact that the d -
orbitals have two nodes, and hence two changes in algebraic sign of ψ, which lead to four lobes.
Related Topics