Chapter: 11th 12th std standard Class Organic Inorganic Physical Chemistry Higher secondary school College Notes

The Wave Nature Of Electrons

It has been made clear that, if a substance is divided into finer and finer pieces, we reach molecules and atoms, then we realize that the atoms consist of electrons and nuclei.

THE WAVE NATURE OF ELECTRONS

It has been made clear that, if a substance is divided into finer and finer pieces, we reach molecules and atoms, then we realize that the atoms consist of electrons and nuclei. It has been clarified that matter is a collection of ultra microscopic particles. Upto the 19th century, these particles were considered to move obeying Newtonian mechanics and Maxwellian electromagnetism. However, this view point has became doubtful after the proposal of the Bohr model of the atomic structure (Bohr's quantum theory).

On the other hand, light had been considered to be electromagnetic waves. However, after the discovery of light quanta (photons), it was clarified that the light has wave nature at one time and particle nature at another time. Therefore, light has a kind of duality.

The idea of deBroglie wave nature waves or deBroglie matter waves is based on the fact that light has both wave and particle nature. Hence particle like electron or proton can also be considered to be 'particle' with 'wave nature'.

Einstein's relations which connect the particle and wave aspects in light quanta

E = hν, p = h / �

would be satisfied for de Broglie matter waves as well. Therefore the relations, Eq.(1), are often called Einstein-de Broglie's relations.

If we apply these relations to the case of the Bohr model of the hydrogen atom, we can well understand its possibility as follows. If we consider that the electron in a hydrogen atom moves at constant speed along a circular orbit around the nucleus (proton), the quantum condition in Bohr's quantum theory is written as Eq(2). By using Einstein's relation p = h/λ in this equation, the quantum condition is written

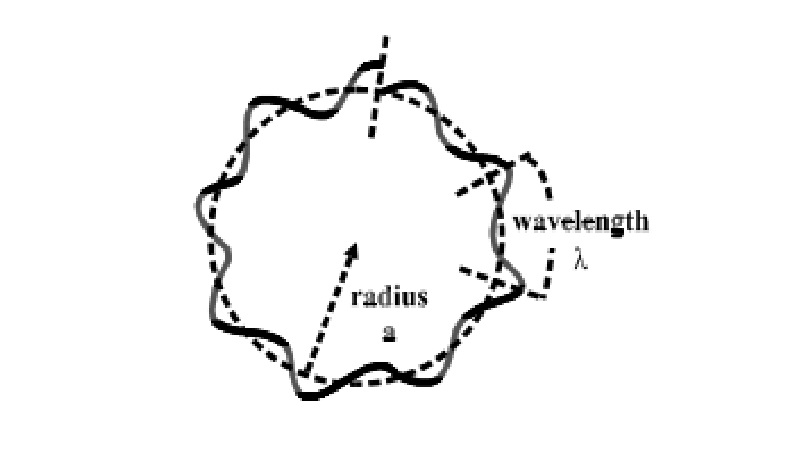
2πa = nλ, (n = 1, 2, 3, ....) (2)

This equation means that the circumference of the circular orbit of the electron must be a integral multiple of the wavelength of de Broglie wave. In other word, de-Broglie wave accompanying the motion of the electron should be continuous. Therefore, we can easily understand the quantum condition that determines the stationary states by considering the continuity of de Broglie waves(fig).

Bohr's quantum condition. The condition for stationary states

The circumference of the circular orbit of the electron should be an integral multiple of the wavelength of de Broglie wave, otherwise the wave cannot be smoothly continuous.

Energy of electron in an atom. By applying Schrodinger wave equation to hydrogen atom, the energy of electron (E_n) was found as :

E_{n = -}2�²me⁴/ h² n²

where n is the principal quantum number. This expression is same as Bohr's equation for energy of electron in a hydrogen atom.

Substituting the values of m, e and h in relation (1), we get

E_{n = -}1312 / n² kJ mol⁻¹

Significance of negative electronic energy

The energy of an electron at infinity is arbitrarily assumed to be zero. This state is called zero-energy state. When an electron moves and comes under the influence of nucleus, it does some work and spends its energy in this process. Thus, the energy of the electron decreases and it becomes less than zero ie., it acquires a negative value.

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

11th 12th std standard Class Organic Inorganic Physical Chemistry Higher secondary school College Notes : The Wave Nature Of Electrons |