Chapter: 11th 12th std standard Class Organic Inorganic Physical Chemistry Higher secondary school College Notes
Calculations based on Principle of Volumetric Analysis
Calculations based on
Principle of Volumetric Analysis
Volumetric Analysis
An important method for determining the amount
of a particular substance is based on measuring the volume of reactant
solution. Suppose substance A in solution reacts with substance B. If you know
the volume and concentration of a solution of B that just reacts with substance
A in a sample, you can determine the amount of A.
Titration is a procedure for determining the
amount of substance A by adding a carefully measured volume of a solution of A
with known concentration of B untill the reaction of A and B is just completed.
Volumetric analysis is a method of analysis based on titrations.
Law
"Equal volume of equinormal solutions exactly neutralise the other
solution having same concentration and volume".
V1 N1 = V2
N2
V1, V2 -
Volume of solutions.
N1, N2 -
Strength of solutions.
Solved problem
Calculating the volume of reactant solution
needed
1. What volume of 6M HCl and 2M HCl should be
mixed to get one litre of 3M HCl?
Solution
Suppose the volume of 6M HCl required to obtain 1L of 3M HCl = XL
Volume of 2M HCl
required = (1-x)L
Applying the
molarity equation
M1V1 + + M2V2 = = M3V3
6MHCl+ 2MHCl=
3MHCl
6x+2(1-x) =
3x1
6x+2-2x =
3
4x =
1
x =
0.25L
hence, volume of
6M HCl required = 0.25L
Volume of 2M HCl
required = 0.75L
2. How much volume of 10M HCl should be diluted with
water to prepare 2.00L of 5M HCl.
Solution
N1V1 = N2V2
10N HCl = 5N
HCl
10xV1 = 5 x
2.00
V1 = (5 x 2.00 )/ 10
= 1.00L
Problems for Practice
1. NiSO4 reacts with Na3PO4 to give a yellow green precipitate of Ni3(PO4)2
and a solution of Na2SO4.
3NiSO4(aq) + 2Na3PO4(aq) Ni3(PO4)2 (s)
+ 3Na2SO4(aq)
How many mL of 0.375M NiSO4 will react with 45.7 mL of 0.265M Na3PO4?
2. What volume of 0.250M HNO3 reacts with 42.4 mL of 0.150M
Na2CO3 in the following reaction?
2HNO3(aq)
+
Na2CO3(aq) 2NaNO3(aq) + H2O(aq)+CO2(g)
3. A flask contains 53.1 mL of 0.150M Ca(OH)2 solution. How many mL of
0.350M Na2CO3 are required to react completely with
Ca(OH)2 in the following reaction.
Na2CO3(aq) + Ca(OH)2(aq)
CaCO3(aq) + 2NaOH(aq)
Determination of
equivalent masses of elements
Equivalent masses can be determined by the following methods:
1. Hydrogen displacement method
2. Oxide method
3. Chloride method
4.
Metal displacement method
1.Hydrogen
displacement method
This method is used to determine the equivalent mass of those metals
such as magnesium, zinc and aluminium which react with dilute acids and readily
displace hydrogen.
Mg + 2HCl -> MgCl2 + H2
Zn + H2SO4 - > ZnSO4 + H2
2Al + 6HCl - > 2AlCl3 +
3H2
From the mass of the metal and the volume of hydrogen displaced, the
equivalent mass of the metal can be calculated.
2.Oxide Method
This method is employed to determine the equivalent mass of those
elements which readily form their oxides eg. magnesium, copper etc. Oxide of an
element can be formed by direct method or by indirect method.
Magnesium forms its oxide directly on heating
2Mg + O2 ® 2 MgO
In the case of copper, its oxide is obtained in an indirect manner i.e.
copper is dissolved in concentrated nitric acid and the copper(II) nitrate
formed after evaporation is strongly heated to give copper (II) oxide.
Cu + 4HNO3 ® Cu(NO3)2 + 2H2O + 2 NO2
2Cu(NO3)2 ® 2CuO + 4 NO2 + O2
Calculations
Mass of the element taken = w1 g
Mass of the oxide of the element = w2 g
Mass of oxygen = (w2-w1) g
(w2
- w1) g of oxygen has combined with w1 g of the metal.
8 g of oxygen
will combine with w1 / (w2 - w1) x 8
This value represents the equivalent mass of the metal.
3.Chloride Method
The equivalent mass of those elements which
readily form their chlorides can be determined by chloride method. For example,
a known mass of pure silver is dissolved completely in dilute nitric acid. The
resulting silver nitrate solution is treated with pure hydrochloric acid when
silver chloride is precipitated. It is then filtered, dried and weighed. Thus
from the masses of the metal and its chloride, the equivalent mass of the metal
can be determined as follows :
4.Calculations
Mass of the metal = w1 g
Mass of the metal chloride = w2 g
Mass of chlorine = (w2 - w2) g
(w2 - w1) g of chlorine has combined with w1
of the metal
35.46 g of chlorine will combine with 35.46 x w1 / (w2 - w1) g of the
metal
This value gives the equivalent mass of the metal.
Uses of volumetric
laws
If the volume of the acid is represented as V1, the normality
of the acid as N1, volume of base as V2 the normality of
the base as N2, then from the law of volumetric analysis it follows
that
V1 x N1 = V2 x N2
All volumetric estimations are based on the
above relationship. If any three quantities are known, the fourth one can readily
be calculated using the above expression.
Equivalent mass of
acid, base, salt, oxidising agent and reducing agent
Acids contain one or more replaceble hydrogen atoms. The number of
replaceble hydrogen atoms present in a molecule of the acid is referred to its
basicity.
1.Equivalent mass of the acid
Equivalent mass of an acid is the number of
parts by mass of the acid which contains 1.008 part by mass of replaceble
hydrogen atom.
Equivalent mass of the
acid = molar
mass of an acid / No. of replaceble hydrogen atom
= molar mass of the acid / basicity of the
acid
For example, the basicity of sulphuric acid is 2.
Equivalent mass of H2SO4 = Molar mass of H2SO4 / 2 = 98/2 = 49
2.Equivalent mass of the base
Equivalent mass of a base is the number of parts by mass of the base
which contains one replaceable hydroxyl ion or which completely
neutralises one gram equivalent of an acid. The number of hydroxyl ions present
in one mole of a base is known as the acidity of the base. Sodium hydroxide,
potassium hydroxide, ammonium hydroxide are examples of monoacidic bases.
Calcium hydroxide is a diacidic base
In general,
equivalent mass of a
base = molar mass of the base /
acidity of the base
Equivalent mass of KOH = 56 /1 = 56
3.Equivalent mass of a
salt
Equivalent mass of a salt is a number of parts by mass of the salt that
is produced by the neutralisation of one equivalent of an acid by a base.
In the case of salt like potassium chloride, the salt formed by the
neutralisation of one equivalent of an acid by a base.
KOH + HCl -> KCl + H2O
Therefore, the equivalent mass of the salt is equal to its molar mass.
4. Equivalent mass of an
oxidising agent
The equivalent mass of an oxidising agent is the number of parts by mass
which can furnish 8 parts by mass of oxygen for oxidation either directly or
indirectly.
For example, potassium permanganate is an oxidising agent. In acid
medium potassium permanganate reacts as follows
2 KMnO4 + 3 H2SO4 ->
K2SO4 + 2
MnSO4 + 3 H2O + 5 [O] 316 80
80 parts by mass of oxygen are made available from 316 parts by mass of
KMnO4
8 parts by
mass of oxygen will be furnished by
(316 x 8 ) / 80 = 3.16
Equivalent mass of KMnO4
= 31.6g equiv-1
5. Equivalent mass of a reducing agent
The equivalent mass of a reducing agent is the number of parts by mass
of the reducing agent which is completely oxidised by 8 parts by mass of oxygen
or with one equivalent of any oxidising agent.
(i) Ferrous sulphate reacts with an oxidising
agent in acid medium according to the equation
2 FeSO4
+ H2SO4 + (O) ® Fe2 (SO4)3 + H2O
2 x 152g
16g
16 parts by mass of oxygen oxidised 304 parts by
mass of ferrous sulphate
8 parts by mass of oxygen will oxidise 304/16 x 8 parts by mass of
ferrous sulphate.
The
equivalent mass of crystalline ferrous sulphate, FeSO4 7H2O is 152 +
126 = 278
126 is the
mass corresponding to 7 moles of water.
(ii) In acid medium, oxalic acid is oxidised according to the equation
(COOH)2 + (O) ® 2 CO2 + H2O
16 Parts by mass of oxygen oxidised 90 parts by
mass of anhydrous oxalic acid.
8 parts by mass of oxygen will oxidise 90/16 x 8
= 45 parts by mass of anhydrous oxalic acid.
Equivalent
mass of anhydrous oxalic acid = 45 g equiv-1
But
equivalent mass of crystalline oxalic acid, (COOH)2. 2H2O=126/2 = 63 g equiv-1.
Determination of
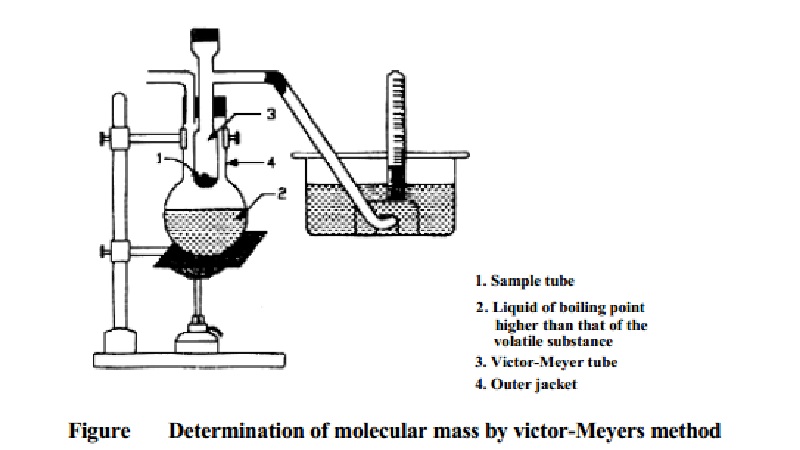
Molecular Mass Victor-Meyer's Method
Principle
In this
method a known mass of a volatile liquid or solid is converted into its vapour
by heating in a Victor-Meyer's tube. The vapour displaces its own volume of
air. The volume of air displaced by the vapour is measured at the experimental
temperature and pressure. The volume of the vapour at s.t.p is then calculated.
From this the mass of 2.24 x 10-2m3 of the vapour at
S.T.P. is calculated. This value represents the molecular mass of the
substance.
method
The apparatus consists of an inner Victor-Meyer tube, the lower end of
which is in the form of a bulb. The upper end of the tube has a side tube which
leads to a trough of water. The Victor-Meyer tube is surrounded by an outer
jacket. In the outer jacket is placed a liquid which boils at a temperature at
least 30 K higher than the boiling point of the volatile substance under study.
A small quantity of glass wool or asbestos fiber covers the bottom of the
Victor-Meyer tube to prevent breakage when the bottle containing the substance
is dropped in.
Procedure
The liquid in the outer jacket is allowed to boil and when no more air
escapes from the side tube, a graduated tube filled with water is inverted over
the side tube dipping in a trough full of water. A small quantity of the
substance is exactly weighed in a small stoppered bottle and quickly dropped in
the heated Victor-Meyer tube and corked immediately.
The bottle
falls on the asbestos pad and its content suddenly changes into vapour, blow
out the stopper and displace an equal volume of air which collects in the
graduated tube. The volume of air in the graduated tube is measured by taking
it out by closing its mouth with the thumb and dipping it in a jar full of water.
When the water levels outside and inside the tube are the same, the volume of
air displaced is noted. The atmospheric pressure and laboratory temperature are
noted.
Calculations
Mass of
the volatile substance = wg
Volume of
air displaced = Volume of vapour = V1 m3
Laboratory
temperature = T1 K
Let the atomospheric pressure be P
Pressure of dry vapour = Atomospheric pressure - aqueous tension at. T1
K Let the aqueous tension be p Nm-2 at that temperature.
Pressure
of dry vapour = P1 = [P-p]
Standard
temperature = T0 = 273 K
Standard
pressure = = P0 = = 1.013 x 105 Nm-2
Let the volume of the vapour at standard temperature and pressure be V0
m3
From the
gas equation, it follows
P0V0 / T0
= P1 V1 / T1
V0 = (P1 V1
/ T1) x (T0/ P0)
The mass of V0 m3 of vapour at s.t.p is w g.
The mass
of 2.24 x 10-2 m3 of the vapour at s.t.p. is
= 2.24x10-2xW
/ V0
The value thus calculatd gives the molecular mass
Molecular mass
= 2 x vapour
density
Vapour
density = Molecular mass / 2
Related Topics