Partial Matching

Partial Matching

For many AI applications complete matching between two or more structures is inappropriate

For example, input representations of speech waveforms or visual scenes may have been corrupted by noise or other unwanted distortions.

In such cases, we do not want to reject the input out of hand. Our systems should be more tolerant of such problems

We want our system to be able to find an acceptable or best match between the input and some reference description

Compensating for Distortions

Finding an object in a photograph given only a general description of the object is a common problems in vision applications

For example, the task may be to locate a human face or human body in photographs without the necessity of storing hundreds of specific face templates

A better approach in this case would be to store a single reference description of the object

Matching between photographs regions and corresponding descriptions then could be approached using either a measure of correlation, by altering the image to obtain a closer fit

If nothing is known about the noise and distortion characteristics, correlation methods can be ineffective or even misleading. In such cases, methods based on mechanical distortion may be appropriate

For example, our reference image is on a transparent rubber sheet. This sheet is moved over the input image and at each location is stretched to get the best match alignment between the two images

The match between the two can then be evaluated by how well they correspond and how much push-and-pull distortion is needed to obtain the best correspondence

Use the number of rigid pieces connected with springs. This pieces can correspond to low level areas such as pixels or even larger area segments

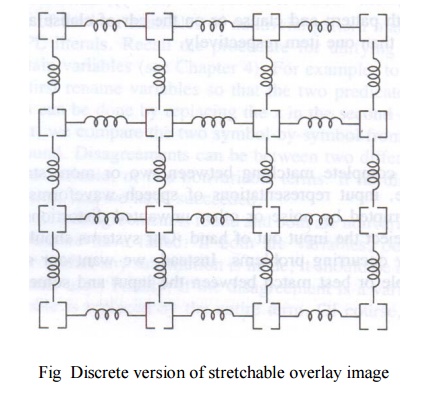
To model any restrictions such as the relative positions of body parts, nonlinear cost functions of piece displacements can be used

The costs can correspond to different spring tensions which reflect the constraints

For example, the cost of displacing some pieces might be zero for no displacement, one unit for single increment displacements in any one of the permissible directions, two units for two position displacements and infinite cost for displacements of more than two increments. Other pieces would be assigned higher costs for unit and larger position displacements when stronger constraints were applicable

The matching problem is to find a least cost location and distortion pattern for the reference sheet with regard to the sensed picture

Attempting to compare each component of some reference to each primitive part of a sensed picture is a combinatorially explosive problem

In using the template-spring reference image and heuristic methods to compare against different segments of the sensed picture, the search and match process can be made tractable

Any matching metric used in the least cost comparison would need to take into account the sum of the distortion costs C_d , the sum of the costs for reference and

sensed component dissimilarities Cc , and the sum of penalty costs for missing components C_m . Thus, the total cost is given by

C_t = C_d + C_c + C_m Finding Match Differences

Distortions occurring in representations are not the only reason for partial matches

For example, in problem solving or analogical inference, differences are expected. In such cases the two structures are matched to isolate the differences in order that they may be reduced or transformed. Once again, partial matching techniques are appropriate

In visual application, an industrial part may be described using a graph structure where the set of nodes correspond to rectangular or cylindrical block subparts

The arc in the graph correspond to positional relations between the subparts

Labels for rectangular block nodes contain length, width and height, while labels for cylindrical block nodes, where location can be above, to the right of, behind, inside and so on

In Fig 8.5 illustrates a segment of such a graph

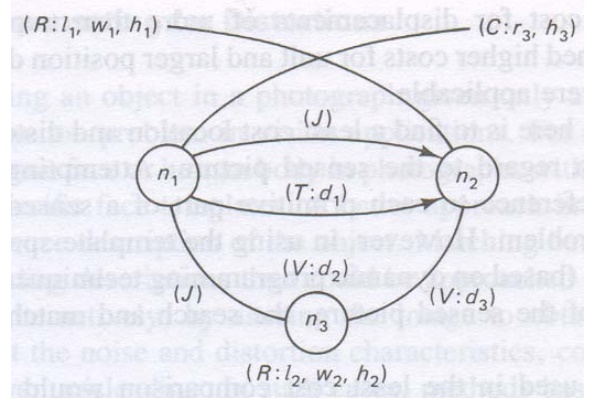
In the fig the following abbreviations are used

Interpreting the graph, we see it is a unit consisting of subparts, mode up of rectangular and cylindrical blocks with dimensions specified by attribute values

The cylindrical block n₁ is to the right of n₂ by d₁ units and the two are connected by a joint

The blocks n₁ and n₂ are above the rectangular block n₃ by d₂ and d₃ units respectively, and so on

Graphs such as this are called attributed relational graphs (ATRs). Such a graph G is defined as a sextuple G = (N, B, A, G_n, G_b)

Where N = { n₁, n₂, . . ., n_k}is a set of nodes, A = {a n₁, an₂, . . . , an_k} is an alphabet of node attributes, B = { b₁, b₂, . . . , b_m}is a set of directed branches (b = (n_i, n_j)), and G_n and G_b are functions for generating node and branch attributes respectively

When the representations are graph structures like ARGs, a similarity measure may be computed as the total cost of transforming one graph into the other

For example, the similarity of two ARGs may be determined with the following steps:

o  Decompose the ARGs into basic subgraphs, each having a depth of one Compute the minimum cost to transform either basic ARG into the other one subgraph-by-subgraph

Compute the total transformation cost from the sum of the subgraph costs

An ARG may be transformed by the three basic operations of node or branch deletions, insertions, or substitutions, where each operation is given a cost based on computation time or other factors