Mixture of gases - Dalton’s law of partial pressures

Mixture of gases - Dalton’s law of partial pressures

Studies of non-reacting gaseous mixtures showed that in a gaseous mixture each component behaves independently. For a gaseous mixture, it is important to know, how the pressure of individual component contributes to the total pressure of the mixture.

John Dalton stated that "the total pressure of a mixture of non-reacting gases is the sum of partial pressures of the gases present in the mixture" where the partial pressure of a component gas is the pressure that it would exert if it were present alone in the same volume and temperature. This is known as Dalton’s law of partial pressures.

i.e., for a mixture containing three gases 1, 2 and 3 with partial pressures p₁, p₂ and p₃ in a container with volume V, the total pressure P_total will be give by

P_total = p₁ + p₂ + p₃ ------- (6.12)

Assuming that the gases behave ideally,

Application of Dalton’s law

In a reaction involving the collection of gas by downward displacement of water, the pressure of dry vapor collected can be calculated using Dalton’s law.

P_{dry gas collected}  = p_total - p_{water vapour}

p_{water vapour} is generally referred as aqueous tension and its values are available

for air at various temperatures.

Let us understand Dalton's law by solving this problem. A mixture of gases contains 4.76 mole of Ne, 0.74 mole of Ar and 2.5 mole of Xe. Calculate the partial pressure of gases, if the total pressure is 2 atm. at a fixed temperature.

Solution:

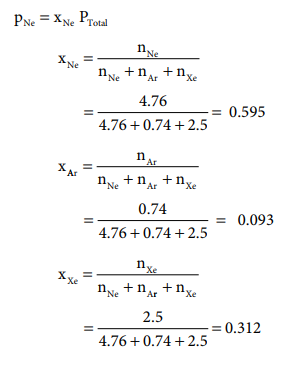
PNe = xNe PTotal = 0.595 × 2 

= 1.19 atm.

P_Ar = x_Ar P_Total = 0.093 × 2

= 0.186 atm.

P_Xe = x_Xe P_Total = 0.312 × 2

= 0.624 atm.

Graham’ s Law of Diffusion

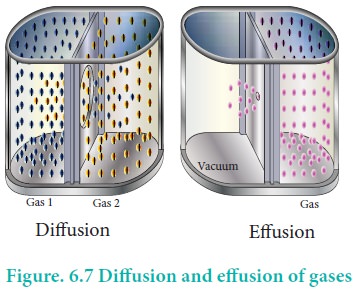
Gases have a tendency to occupy all the available space. When two non -reactive gases are allowed to mix, the gas molecules migrate from region of higher concentration to a region of lower concentration. This property of gas which involves the movement of the gas molecules through another gases is called diffusion. Effusion is another process in which a gas escapes from a container through a very small hole. The rate of diffusion or effusion is inversely proportional to the square root of molar mass. This statement is called Graham's law of diffusion/effusion.

where r_A and r_B are the rates of diffusion of A and B and the M_A and M_B are their respective molar masses.

1. An unknown gas diffuses at a rate of 0.5 time that of nitrogen at the same  temperature and pressure. Calculate the molar mass of the unknown gas

Solution: