MIN-MAX Search Algorithm

MIN-MAX Search

Games have always been an important application area for heuristic algorithms. In playing games whose state space may be exhaustively delineated, the primary difficulty is in accounting for the actions of the opponent. This can be handled easily by assuming that the opponent uses the same knowledge of the state space as us and applies that knowledge in a consistent effort to win the game. Minmax implements game search under referred to as MIN and MAX.

The min max search procedure is a depth first, depth limited search procedure. The idea is to start at the current position and use the plausible move generator to generate the set of possible successor positions. To decide one move, it explores the possibilities of winning by looking ahead to more than one step. This is called a ply. Thus in a two ply search, to decide the current move, game tree would be explored two levels farther.

Consider the below example

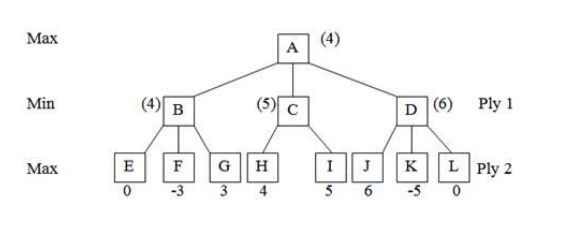
Figure Tree showing two ply search

In this tree, node A represents current state of any game and nodes B, C and D represent three possible valid moves from state A. similarly E, F, G represents possible moves from B, H, I from C and J, K, L, from D. to decide which move to be taken from A, the different possibilities are explored to two next steps. 0, -3, 3, 4, 5, 6, -5, 0 represent the utility values of respective move. They indicate goodness of a move. The utility value is back propagated to ancestor node, according to situation whether it is max ply or min ply. As it is a two player game, the utility value is alternatively maximized and minimized. Here as the second player’s move is maximizing, so maximum value of all children of one node will be back propagated to node. Thus, the nodes B, C, D, get the values 4, 5, 6 respectively. Again as ply 1 is minimizing, so the minimum value out of these i.e. 4 is propagated to A. then from A move will be taken to B.

MIN MAX procedure is straightforward recursive procedure that relies on two auxiliary procedures that are specific to the game being played.

1.    MOVEGEN (position, player): the move generator which returns a list of nodes representing the moves that can be made by player in position. We may have 2 players namely PLAYER-TWO in a chess problem.

2.    STATIC (position, player): the static evaluation function, which returns a number representing the goodness of position from the standpoint of player.

We assume that MIN MAX returns a structure containing both results and that we have two functions, VALUE and PATH that extract the separate components. A function LAST PLY is taken which is assumed to evaluate all of the factors and to return TRUE if the search should be stopped at the current level and FALSE otherwise.

MIN MAX procedure takes three parameters like a board position, a current depth of the search and the players to move. So the initial call to compute the best move from the position CURRENT should be

MIN MAX (CURRENT, 0, PLAYER-ONE)

(If player is to move)

Or

MIN MAX (CURRENT, 0, PLAYER-TWO)

(If player two is to move)

Let us follow the algorithm of MIN MAX

Algorithm: MINMAX (position, depth, player)

1.     If LAST PLY (position, depth)

Then RETURN VALUE = STATIC (position, player) PATH = nil.

2.     Else, generate one more ply of the tree by calling the function MOVE_GEN (position, player) and set SUCCESORS to the list it returns.

3.     If SUCESSORS is empty,

THEN no moves to be made

RETURN the same structure that would have been returned if LAST_PLY had returned TRUE.

4.     If SUCCESORS is not empty,

THEN examine each element in turn and keep track of the best one.

5.     After examining all the nodes,

RETURNVALUE          = BEST- SCORE

PATH         = BEST- PATH

When the initial call to MIN MAX returns, the best move from CURRENT is the first element in the PATH.

Alpha- Beta (α-β) Pruning

When a number of states of a game increase and it cannot be predicted about the states, then we can use the method pruning. Pruning is a method which is used to reduce the no. of states in a game. Alpha- beta is one such pruning technique. The problem with minmax search is that the number of game states it has to examine is exponential in the number of moves. Unfortunately we cannot eliminate the exponent, but we can effectively cut it in half. Alpha-beta pruning is one of the solutions to the problem of minmax search tree. When α-β pruning is applied to a standard minmax tree, it returns the same move as minmax would, but prunes away branches that cannot possibly influence the final decision.

The idea of alpha beta pruning is very simple. Alpha beta search proceeds in a depth first fashion rather than searching the entire space. Generally two values, called alpha and beta, are created during the search. The alpha value is associated with MAX nodes and the beta value is with MIN values. The value of alpha can never decrease; on the other hand the value of beta never increases. Suppose the alpha value of A MAX node is 5. The MAX node then need not consider any transmitted value less than or equal to 5 which is associated with any MIN node below it. Alpha is the worst that MAX can score given that MIN will also do its best. Similarly, if a MIN has a beta value of 5, it need not further consider any MAX node below it that has a value of 6 or more.

The general principal is that: consider a node η somewhere in the search tree, such that player has a choice of moving to that node. If player has a better choice К either at the parent node of η or at any choice point further up, then η will never be reached in actual play. So once we have found out enough about η (by examining some of its descendents) to reach this conclusion, we can prune it.

We can also say that “ α” is the value of the best choice we have found so far at any choice point along the path for MAX. Similarly “ β” is the value of the best choice we have found so far at any choice point along the path for MIN. Consider the following example

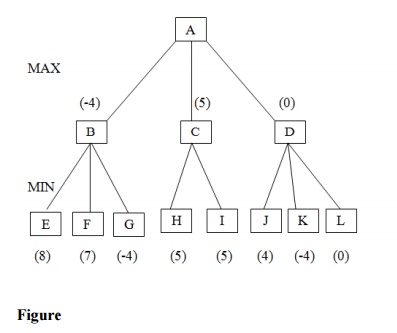
Here at MIN ply, the best value from three nodes is - 4, 5, 0. These will be back propagated towards root and a maximizing move 5 will be taken. Now the node E has the value 8 is far more, then accepted as it is minimizing ply. So, further node E will not be explored. In the situation when more plies are considered, whole sub tree below E will be pruned. Similarly if α=0, β=7, all the nodes and related sub trees having value less than 0 at maximizing ply and more than 7 at minimizing ply will be pruned.

Alpha beta search updates the value of α and β as it goes along and prunes the remaining branches at a node as soon as the value of the current node is known to be worse than the current α and β value for MAX or MIN respectively. The effectiveness of alpha- beta pruning is highly dependent on the order in which the successors are examined suppose in a search tree the branching factor is x and depth d. the α-β search needs examining only x^0/9 nodes to pick up best move, instead of x⁰ for MINMAX.