Logical Agents

LOGICAL AGENTS

Knowledge representation

A variety of ways of knowledge (facts) have been exploited in AI programs. Facts: truths in some relevant world. These are things we want to represent.

Propositional logic

It is a way of representing knowledge.In logic and mathematics, a propositional calculus or logic is a formal system in which formulae representing propositions can be formed by combining atomic propositions

using logical connectives

Sentences considered in propositional logic are not arbitrary sentences but are the ones that are either true or false, but not both. This kind of sentences are called propositions.

Example

Some facts in propositional logic:

It is raining. - RAINING

It is sunny - SUNNY

It is windy - WINDY

If it is raining ,then it is not sunny - RAINING -> SUNNY

Elements of propositional logic

Simple sentences which are true or false are basic propositions. Larger and more complex sentences are constructed from basic propositions by combining them with connectives. Thus propositions and connectives are the basic elements of propositional logic. Though there are many connectives, we are going to use the following five basic connectives here: NOT, AND, OR, IF_THEN (or IMPLY), IF_AND_ONLY_IF. They are also denoted by the symbols: , , , , , respectively.

Inference

Inference is deriving new sentences from old.

Modus ponens

There are standard patterns of inference that can be applied to derive chains of conclusions that lead to the desired goal. These patterns of inference are called inference

rules.

Entailment

Propositions tell about the notion of truth and it can be applied to logical reasoning. We can have logical entailment between sentences. This is known as entailment where a sentence follows logically from another sentence.In mathematical notation we write : knowledge based agents or logical agents.The central component of a knowledge-based agent is its knowledge base, or KB.

Informally,a knowledge base is a set of sentences. Each sentence is expressed in language called a knowledge representation language and represents some assertion about the world.

The syntax of propositional logic defines the allowable sentences. The atomic sentences-

the indivisible syntactic elements-consist of a single proposition symbol. Each such symbol tands for a proposition that can be true or false. We will use uppercase names for symbols: P, Q, R, and so on.

Complex sentences are constructed from simpler sentences using logical connectives. There are five connectives in common use:

First order Logic

Whereas propositional logic assumes the world contains facts, first-order logic (like natural language) assumes the world contains

Objects: people, houses, numbers, colors, baseball games, wars, …

Relations: red, round, prime, brother of, bigger than, part of, comes between, Functions: father of, best friend, one more than, plus,

The basic syntactic elements of -orderlogicare. the symbols that stand for objects, relations, and functions. The symbols,come in three kinds:

a) constant symbols, which stand for objects;

b) predicate symbols, which stand for relations;

c) and function symbols, which stand for functions.

We adopt the convention that these symbols will begin with uppercase letters.

Example: Constant symbols : Richard

and John; predicate symbols :

Brother, OnHead, Person, King, and

Crown; function symbol :LeftLeg.

Quantifiers

There is need to express properties of entire collections of objects,instead of enumerating the objects by name. Quantifiers let us do this.FOL contains two standard quantifiers called

a) Universal (  ) and

b) Existential (  )

Universal quantification

( x) P(x) : means that P holds forall values of x in the domain associated with that variable

E.g., ( x) dolphin(x) => mammal(x)

Existential quantification

(  x)P(x) means that P holds for some value of x in the domain associated with that

variable

E.g., ( x) mammal(x) ^ lays-eggs(x)

Permits one to make a statement about some object without naming it

Explain Universal Quantifiers with an example.

Rules such as "All kings are persons,'' is written in first-order logic as

x King(x) => Person(x)

where is pronounced as “ For all ..”

Thus, the sentence says, "For all x, if x is a king, then z is a person." The symbol x is called a variable(lower case letters)

The sentence x P,where P is a logical expression says that P is true for every object x.

Existential quantifiers with an example.

Universal quantification makes statements about every object. It is possible to make a statement about some object in the universe without naming it,by using an existential quantifier.

Example

“King John has a crown on his head” x Crown(x) ^ OnHead(x,John)

x is pronounced There“ exists an x such that ..” or “ For some x ..” connection between universal and existential quantifiers

“Everyone likes icecream “ is equivalent “there is no one who does not like icecream”

This can be expressed as :

x Likes(x,IceCream) isquivalent to Likes(x,IceCream)

STEPS ASSOCIATED WITH THE KNOWLEDGE  ENGINEERING PROCESS

Knowledge Engineering

Discuss them by applying the steps to any real world application of your choice. The general process of knowledge base construction a process is called knowledge engineering. A knowledge engineer is someone who investigates a particular domain, learns what concepts are important in that domain, and creates a formal representation of the objects and relations in the domain. We will illustrate the knowledge engineering process in an electronic circuit domain that should already be fairly familiar,

The steps associated with the knowledge engineering process are :

1. Identfy the task.

. The task will determine what knowledge must be represented in order to connect problem instances to answers. This step is analogous to the PEAS process for designing agents.

2.  Assemble the relevant knowledge. The knowledge engineer might already be an expert in the domain, or might need to work with real experts to extract what they know-a process called knowledge acquisition.

3.  Decide on a vocabulary of predicates, functions, and constants. That is, translate the important domain-level concepts into logic-level names.

Once the choices have been made. the result is a vocabulary that is known as the ontology of the domain. The word ontology means a particular theory of the nature of being or existence.

4. Encode general /knowledge about the domain.

The knowledge engineer writes down the axioms for all the vocabulary terms. This pins down (to the extent possible) the meaning of the terms, enabling the expert to check the content. Often, this step reveals misconceptions or gaps in the vocabulary that must be fixed by returning to step 3 and iterating through the process.

5. Encode a description of the specific problem instance.

For a logical agent, problem instances are supplied by the sensors, whereas a "disembodied" knowledge base is supplied with additional sentences in the same way that traditional programs are supplied with input data.

6. Pose queries to the inference procedure and get answers.

This is where the reward is: we can let the inference procedure operate on the axioms and problem-specific facts to derive the facts we are interested in knowing.

7. Debug the knowledge base.

x NumOfLegs(x,4) => Mammal(x) Is false for reptiles ,amphibians.

To understand this seven-step process better, we now apply it to an extended example-the domain of electronic circuits.

The electronic circuits domain

We will develop an ontology and knowledge base that allow us to reason about digital Circuits of the kind shown in Figure 8.4. We follow the seven-step process for knowledge engineering There are many reasoning tasks associated with digital circuits. At the highest level, one analyzes the circuit's functionality. For example, what are all the gates connected to the first input terminal? Does the circuit contain feedback loops? These will be our tasks in this section.

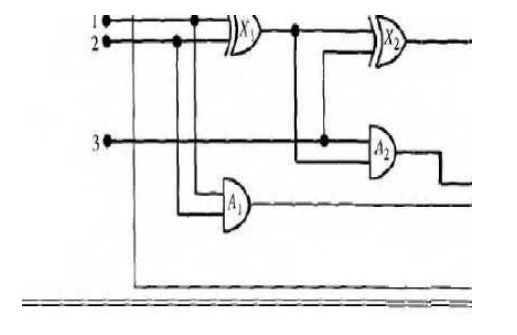
Assemble the relevant knowledge

What do we know about digital circuits? For our purposes, they are composed of wires and gates. Signals flow along wires to the input terminals of gates, and each gate produces a decide

on vocabulary.

We now know that we want to talk about circuits, terminals, signals, and gates. The next step is to choose functions, predicates, and constants to represent them. We will start from individual gates and move up to circuits. First, we need to be able to distinguish a gate from other gates. This is handled by naming gates with constants: X I , X2, and so on

Encode general knowledge of the domain

One sign that we have a good ontology is that there are very few general rules which need to be specified. A sign that we have a good vocabulary is that each rule can be stated clearly and concisely. With our example, we need only seven simple rules to describe everything we need to know about circuits:

1. If two terminals are connected, then they have the same signal:

2. The signal at every terminal is either 1 or 0 (but not both):

3. Connected is a commutative predicate:

4. An OR gate's output is 1 if and only if any of its inputs is 1:

5. An A.ND gate's output is 0 if and only if any of its inputs is 0:

6. An XOR gate's output is 1 if and only if its inputs are different:

7. A NOT gate's output is different from its input:

Encode the specific problem instance

The circuit shown in Figure 8.4 is encoded as circuit C1 with the following description.

First, we categorize the gates:

Type(X1)= XOR Type(X2)= XOR

Pose queries to the inference procedure

What combinations of inputs would cause the first output of Cl (the sum bit) to be 0 and The second output of C1 (the carry bit) to be l?

Debug the knowledge base

We can perturb the knowledge base in various ways to see what kinds of erroneous

behaviors

emerge.

Usage of First Order Logic.

The best way to find usage of First order logic is through examples. The examples can be taken from some simple domains. In knowledge representation, a domain is just some part of

the world about which we wish to express some knowledge.

Assertions and queries in first-order logic

Sentences are added to a knowledge base using TELL, exactly as in propositional logic.

Such

sentences are called assertions.

For example, we can assert that John is a king and that kings are persons:

TELL(KB, King (John))

Where KB is knowledge base.

TELL(KB, x King(x) => Person(x)).

We can ask questions of the knowledge base using ASK. For example, returns true.

Questions asked using ASK are called queries or goals ASK(KB,Person(John))

Will return true.

(ASK KBto find whther Jon is a king) ASK(KB, x person(x))

.

The kinship domain

The first example we consider is the domain of family relationships, or kinship. This domain includes facts such as

"Elizabeth is the mother of Charles" and

"Charles is the father of William7' and rules such as "One's grandmother is the mother of one's parent." Clearly, the objects in our domain are people.

We will have two unary predicates, Male and Female.

Kinship relations-parenthood, brotherhood, marriage, and so on-will be represented by binary predicates: Parent, Sibling, Brother, Sister, Child, Daughter,Son, Spouse, Husband, Grandparent, Grandchild, Cousin, Aunt, and Uncle.

We will use functions for Mother and Father.

Forward chaining with an example.

Using a deduction to reach a conclusion from a set of antecedents is called forward chaining. In other words,the system starts from a set of facts,and a set of rules,and tries to find the way of using these rules and facts to deduce a conclusion or come up with a suitable couse of action. This is known as data driven reasoning.

The proof tree generated by forward chaining.

Example knowledge base

• The law says that it is a crime for an American to sell weapons to hostile nations. The

country Nono, an enemy of America, hassomemissiles, and all of its missiles were sold to it by Colonel West, who is American.

• Prove that Col. West is a criminal

... it is a crime for an American to sell weapons to hostile nations: American(x)

Note:

(a)The initial facts appear in the bottom level

(b) Facts inferred on the first iteration is in the middle level

(c) The facts inferered on the 2nd iteration is at the top level

ALGORITHM

Backward chaining with an example.

Forward chaining applies a set of rules and facts to deduce whatever conclusions can be derived. In backward chaining ,we start from a conclusion, which is the hypothesis we wish to prove and we aim to show how that conclusion can be reached from the rules and facts in the data base. The conclusion we are aiming to prove is called a goal, and the reasoning in this way is known as goal-driven.

Backward chaining example

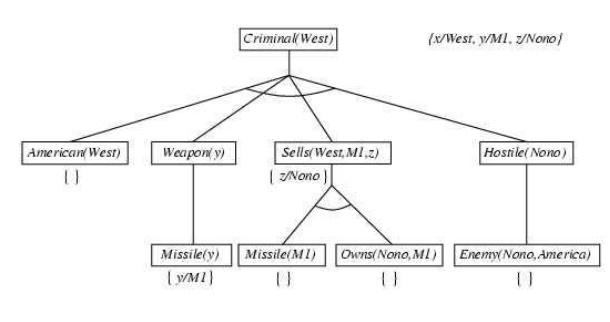
Note:

(a)              To prove Criminal(West) ,we have to prove four conjuncts below it.

(b)             Some of which are in knowledge base,and others require further backward

UNIFICATION:

UNIFY(P,R)=UNIFY(Q,R)=UNIFY(P,Q)

RESOLUTION:

v NF

v CNF

v INF WITH REFUTATION

v CNF WITH REFUTATION