Induction Law - Transformer

Induction Law

The voltage induced across the secondary coil may be calculated from Faraday's law of  induction, which states that:

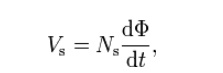
where Vs is the instantaneous voltage, Ns is the number of turns in the secondary coil and Φ is the magnetic flux through one turn of the coil. If the turns of the coil are oriented perpendicularly to the magnetic field lines, the flux is the product of the magnetic flux density B and the area A through which it cuts. The area is constant, being equal to the cross-sectional area of the transformer core, whereas the magnetic field varies with time according to the excitation of the primary. Since the same magnetic flux passes through both the primary and secondary coils in an ideal transformer, the instantaneous voltage across the primary winding equals

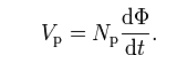
Taking the ratio of the two equations for Vs and Vp gives the basic equation for stepping up or stepping down the voltage

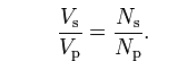
Np/Ns is known as the turns ratio, and is the primary functional characteristic of any transformer. In the case of step-up transformers, this may sometimes be stated as the reciprocal, Ns/Np. Turns ratio is commonly expressed as an irreducible fraction or ratio: for example, a transformer with primary and secondary windings of, respectively, 100 and 150 turns is said to have a turns ratio of 2:3 rather than 0.667 or 100:150.

An elementary transformer consists of a soft iron or silicon steel core and two windings, placed on it. The windings are insulated from both the core and each other. The core is built up of thin soft iron or low reluctance to the magnetic flux. The winding connected to the magnetic flux. The winding connected to the supply main is called the primary and the winding connected to the load circuit is called the secondary.

Although in the actual construction the two windings are usually wound one over the other, for the sake of simplicity, the figures for analyzing transformer theory show the windings on opposite sides of the core, as shown below Simple Transformer

.

When primary winding is connected to an ac supply mains, current flows through it. Since this winding links with an iron core, so current flowing through this winding produces an alternating flux in the core. Since this flux is alternating and links with the secondary winding also, so induces an emf in the secondary winding.

The frequency of induced emf in secondary winding is the same as that of the flux or that of the s supply voltage. The induced emf in the secondary winding enables it to deliver current to an external load connected across it. Thus the energy is transformed from primary winding to the secondary winding by means of electro-magnetic induction without anychange in frequency. The flux of the iron core links not only with the secondary winding but also with the primary winding, so produces self-induced emf in the primary winding:

This induced in the primary winding opposes the applied voltage and therefore sometimes it is known as back emf of the primary. In fact the induced emf in the primary winding limits the primary current in much the same way that the back emf in a dc motor limits the armature current.

Transformation ratio.

The ratio of secondary voltage to primary voltage is known as the voltage transformation ratio and is designated by letter K. i.e. Voltage transformation ratio.

Current ratio.

The ratio of secondary current to primary current is known as current ratio and is reciprocal of voltage transformation ratio in an ideal transformer.