Heuristic Repair

Heuristic Repair

Heuristics can be used to improve performance of solutions to constraint satisfaction problems.

One way to do this is to use a heuristic repair method, which involves generating a possible solution (randomly, or using a heuristic to generate a position that is close to a solution) and then making changes that reduce the distance of the state from the goal.

In the case of the eight-queens problem, this could be done using the minconflicts heuristic.

To move from one state to another state that is likely to be closer to a solution using the min-conflicts heuristic, select one queen that conflicts with another queen (in other words, it is on the same row, column, or diagonal as another queen).

Now move that queen to a square where it conflicts with as few queens as possible. Continue with another queen. To see how this method would work, consider the starting position shown in Fig 6.3.

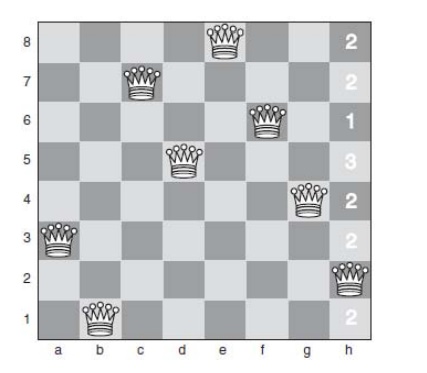
This starting position has been generated by placing the queens such that there are no conflicts on rows or columns. The only conflict here is that the queen in column 3 (on c7) is on a diagonal with the queen in column h (on h2).

To move toward a solution, we choose to move the queen that is on column h.

We will only ever apply a move that keeps a queen on the same column because we already know that we need to have one queen on each column.

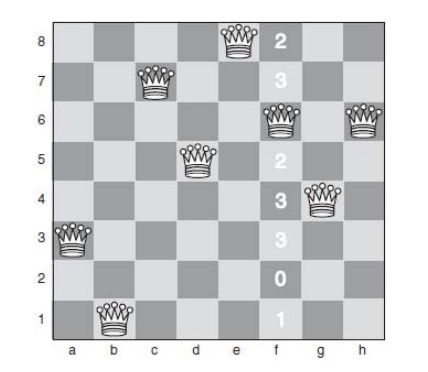
Each square in column h has been marked with a number to show how many other queens that square conflicts with. Our first move will be to move the queen on column h up to row 6, where it will conflict only with one queen. Then we arrive at the position shown in below Fig

Because we have created a new conflict with the queen on row 6 (on f6), our next move must be to move this queen. In fact, we can move it to a square where it has zero conflicts. This means the problem has been solved, and there are no remaining conflicts.

This method can be used not only to solve the eight-queens problem but also has been successfully applied to the n-queens problem for extremely large values of n. It has been shown that, using this method, the 1,000,000 queens problem can be solved in an average of around 50 steps.

Solving the 1,000,000-queens problem using traditional search techniques would be impossible because it would involve searching a tree with a branching factor of 10¹².

Local Search and Metaheuristics

Local search methods work by starting from some initial configuration (usually random) and making small changes to the configuration until a state is reached from which no better state can be achieved.

Hill climbing is a good example of a local search technique.

Local search techniques, used in this way, suffer from the same problems as hill climbing and, in particular, are prone to finding local maxima that are not the best solution possible.

The methods used by local search techniques are known as metaheuristics.

Examples of metaheuristics include simulated annealing, tabu search, genetic algorithms, ant colony optimization, and neural networks.

This kind of search method is also known as local optimization because it is attempting to optimize a set of values but will often find local maxima rather than a global maximum.

A local search technique applied to the problem of allocating teachers to classrooms would start from a random position and make small changes until a configuration was reached where no inappropriate allocations were made.

Exchanging Heuristics

The simplest form of local search is to use an exchanging heuristic.

       An exchanging heuristic moves from one state to another by exchanging one or more variables by giving them different values. We saw this in solving the eight-queens problem as heuristic repair.

       A k-exchange is considered to be a method where k variables have their values changed at each step.

       The heuristic repair method we applied to the eight-queens problem was 2-exchange.

       A k-exchange can be used to solve the traveling salesman problem. A tour (a route through the cities that visits each city once, and returns to the start) is generated at random. Then, if we use 2-exchange, we remove two edges from the tour and substitute them for two other edges. If this pro duces a valid tour that is shorter than the previous one, we move on from here. Otherwise, we go back to the previous tour and try a different set of substitutions.

       In fact, using k = 2 does not work well for the traveling salesman problem, whereas using k = 3 produces good results.

       Using larger numbers of k will give better and better results but will also require more and more iterations.

       Using k = 3 gives reasonable results and can be implemented efficiently. It does, of course, risk finding local maxima, as is often the case with local search methods.

Iterated Local Search

       Iterated local search techniques attempt to overcome the problem of local maxima by running the optimization procedure repeatedly, from different initial states.

       If used with sufficient iterations, this kind of method will almost always find a global maximum.

       The aim, of course, in running methods like this is to provide a very good solution without needing to exhaustively search the entire problem space.

In problems such as the traveling salesman problem, where the search space grows extremely quickly as the number of cities increases, results can be generated that are good enough (i.e., a local maximum) without using many iterations, where a perfect solution would be impossible to find (or at least it would be impossible to guarantee a perfect solution even one iteration of local search may happen upon the global maximum).