Constraint Satisfaction Search

Constraint Satisfaction Search

Search can be used to solve problems that are limited by constraints, such as the eight-queens problem. Such problems are often known as Constraint Satisfaction Problems, or CSPs. I n this problem, eight queens must be placed on a chess board in such a way that no two queens are on the same diagonal, row, or column. If we use traditional chess board notation, we mark the columns with letters from a to g and the rows with numbers from 1 to 8. So, a square can be referred to by a letter and a number, such as a4 or g7.

This kind of problem is known as a constraint satisfaction problem (CSP) because a solution must be found that satisfies the constraints.

In the case of the eight-queens problem, a search tree can be built that represents the possible positions of queens on the board. One way to represent this is to have a tree that is 8-ply deep, with a branching factor of 64 for the first level, 63 for the next level, and so on, down to 57 for the eighth level.

A goal node in this tree is one that satisfies the constraints that no two queens can be on the same diagonal, row, or column.

An extremely simplistic approach to solving this problem would be to analyze every possible configuration until one was found that matched the constraints.

A more suitable approach to solving the eight-queens problem would be to use depth-first search on a search tree that represents the problem in the following manner:

      The first branch from the root node would represent the first choice of a square for a queen. The next branch from these nodes would represent choices of where to place the second queen.

      The first level would have a branching factor of 64 because there are 64 possible squares on which to place the first queen. The next level would have a somewhat lower branching factor because once a queen has been placed, the constraints can be used to determine possible squares upon which the next queen can be placed.

The branching factor will decrease as the algorithm searches down the tree. At some point, the tree will terminate because the path being followed will lead to a position where no more queens can be placed on legal squares on the board, and there are still some queens remaining.

In fact, because each row and each column must contain exactly one queen, the branching factor can be significantly reduced by assuming that the first queen must be placed in row 1, the second in row 2, and so on. In this way, the first level will have a branching factor of 8 (a choice of eight squares on which the first queen can be placed), the next 7, the next 6, and so on.

The search tree can be further simplified as each queen placed on the board “uses up” a diagonal, meaning that the branching factor is only 5 or 6 after the first choice has been made, depending on whether the first queen is placed on an edge of the board (columns a or h) or not.

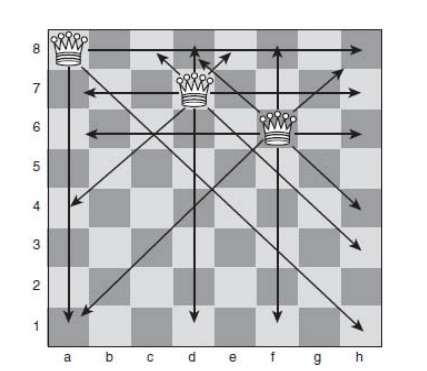
The next level will have a branching factor of about 4, and the next may have a branching factor of just 2, as shown in Fig 6.1.

The arrows in Fig 6.1 show the squares to which each queen can move.

Note that no queen can move to a square that is already occupied by another queen.

In Fig 6.1, the first queen was placed in column a of row 8, leaving six choices for the next row. The second queen was placed in column d of row 7, leaving four choices for row 6. The third queen was placed in column f in row 6, leaving just two choices (column c or column h) for row 5.

Using knowledge like this about the problem that is being solved can help to significantly reduce the size of the search tree and thus improve the efficiency of the search solution.

A solution will be found when the algorithm reaches depth 8 and successfully places the final queen on a legal square on the board.

A goal node would be a path containing eight squares such that no two squares shared a diagonal, row, or column.

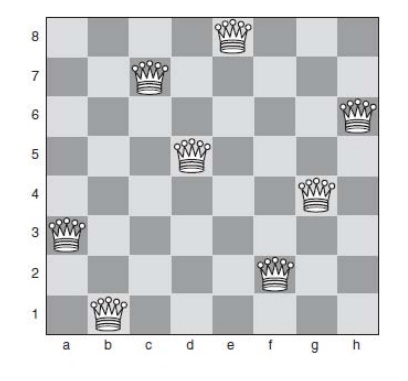
One solution to the eight-queens problem is shown in above Fig .

Note that in this solution, if we start by placing queens on squares e8, c7, h6, and then d5, once the fourth queen has been placed, there are only two choices for placing the fifth queen (b4 or g4). If b4 is chosen, then this leaves no squares that could be chosen for the final three queens to satisfy the constraints. If g4 is chosen for the fifth queen, as has been done in Fig 6.2, only one square is available for the sixth queen (a3), and the final two choices are similarly constrained. So, it can be seen that by applying the constraints appropriately, the search tree can be significantly reduced for this problem.

Using chronological backtracking in solving the eight-queens problem might not be the most efficient way to identify a solution because it will backtrack over moves that did not necessarily directly lead to an error, as well as ones that did. In this case, nonchronological backtracking, or dependency-directed backtracking could be more useful because it could identify the steps earlier in the search tree that caused the problem further down the tree.

Forward Checking

In fact, backtracking can be augmented in solving problems like the eightqueens problem by using a method called forward checking.

As each queen is placed on the board, a forward-checking mechanism is used to delete from the set of possible future choices any that have been rendered impossible by placing the queen on that square.

For example, if a queen is placed on square a1, forward checking will remove all squares in row 1, all squares in column a, and also squares b2, c3, d4, e5, f6, g7, and h8.

In this way, if placing a queen on the board results in removing all remaining squares, the system can immediately backtrack, without having to attempt to place any more queens.

This can often significantly improve the performance of solutions for CSPs such as the eight-queens problem.

Most-Constrained Variables

A further improvement in performance can be achieved by using the most-constrained variable heuristic.

At each stage of the search, this heuristic involves working with the variable that has the least possible number of valid choices.

In the case of the eight-queens problem, this might be achieved by considering the problem to be one of assigning a value to eight variables, a through h. Assigning value 1 to variable a means placing a queen in square a1.

To use the most constrained variable heuristic with this representation means that at each move we assign a value to the variable that has the least choices available to it. Hence, after assigning a = 1, b = 3, and c = 5, this leaves three choices for d, three choices for e, one choice for f, three choices for g, and three choices for h. Hence, our next move is to place a queen in column f.

This heuristic is perhaps more clearly understood in relation to the mapcoloring problem. It makes sense that, in a situation where a particular country can be given only one color due to the colors that have been assigned to its neighbors, that country be colored next.

The most-constraining variable heuristic is similar in that it involves assigning a value next to the variable that places the greatest number of constraints on future variables.

The least-constraining value heuristic is perhaps more intuitive than the two already presented in this section.

This heuristic involves assigning a value to a variable that leaves the greatest number of choices for other variables.

This heuristic can be used to make n-queens problems with extremely large values of n quite solvable.

Example: Cryptographic Problems

The constraint satisfaction procedure is also a useful way to solve problems such as cryptographic problems. For example:

FORTY

                              TEN

                              TEN

SIXTY

Solution:

29786

                              850

                              850

31486

This cryptographic problem can be solved by using a Generate and Test method, applying the following constraints:

      Each letter represents exactly one number.

      No two letters represent the same number.

Generate and Test is a brute-force method, which in this case involves cycling through all possible assignments of numbers to letters until a set is found that meets the constraints and solves the problem.

Without using constraints, the method would first start by attempting to assign 0 to all letters, resulting in the following sum:

00000

                              000

                              000

00000

Although this may appear to be a valid solution to the problem, it does not meet the constraints laid down that specify that each letter can be assigned only one number, and each number can be assigned only to one letter.

Hence, constraints are necessary simply to find the correct solution to the problem. They also enable us to reduce the size of the search tree.

In this case, for example, it is not necessary to examine possible solutions where two letters have been assigned the same number, which dramatically reduces the possible solutions to be examined.