Fresnel’s distance

Fresnel’s distance

Fresnel’s distance is the distance up to which the ray optics is valid in terms of rectilinear propagation of light. As there is bending of light in diffraction, the rectilinear propagation of light is violated. But, this bending is not significant till the diffracted ray crosses the central maximum at a distance z as shown in Figure 6.65. Hence, Fresnel’s distance is the distance upto which ray optics is obeyed and beyond which ray optics is not obeyed but, wave optics becomes significant.

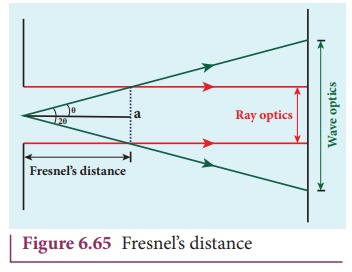
From the diffraction equation for first minimum, sinθ = λ/a; Î¸ = λ/a

From the definition of Fresnel’s distance, sin2θ = a/z; 2θ = a/z

Equating the above two equation gives, Î»/a=a/2z

After rearranging, we get Fresnel’s distance z as,

EXAMPLE 6.33

Calculate the distance for which ray optics is good approximation for an aperture of 5 mm and wavelength 500 nm.

Solution

a = 5 mm = 5 × 10-3 m;

λ = 500nm = 500×10−9 m; z = ?

Equation for Fresnel’s distance, z = a2/2λ

Substituting,

z = [5 × 10-3]2 / 2×500×10−9

z = 25 m