Constraint Satisfaction Problems (CSPS)

CONSTRAINT SATISFACTION PROBLEMS (CSPS)

•                      Standard search problem:

– state is a "black box“ – any data structure that supports successor function, heuristic function, and goal test

•                      CSP:

–  state is defined by variables Xi with values from domain Di

– goal test is a set of constraints specifying allowable combinations of values for subsets of variables

–  Simple example of a formal representation language

•                      Allows useful general-purpose algorithms with more power than standard search algorithms

Arc consistency:

1.                                  Arc refers to a directed arc in the constraint graph.

2.                                  Arc consistency checking can be applied either as a preprocessing. step before the process must be applied repeatedly until no more inconsistency remain.

Path consistency:

Path consistency means that any pair of adjacent variables can always be extended to a third neighboring variable, this is also called path consistency

K-consistency:

Stronger forms of propagation can be defined using the notation called K-consistency. A CSP is K-consistency if for any set of K-1 variables and for any consistent assignment to those variables, a constant value can always be assigned to any variable.

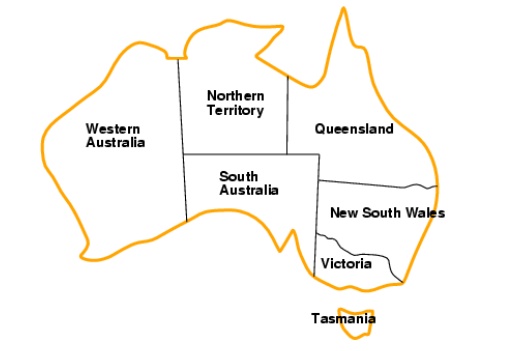
Example: Map-Coloring

•                      Variables WA, NT, Q, NSW, V, SA, T

•                      Domains Di = {red,green,blue}

•                      Constraints: adjacent regions must have different colors

e.g., WA ≠ NT, or (WA,NT) in ,(red,green),(red,blue),(green,red), (green,blue),(blue,red),(blue,green)}

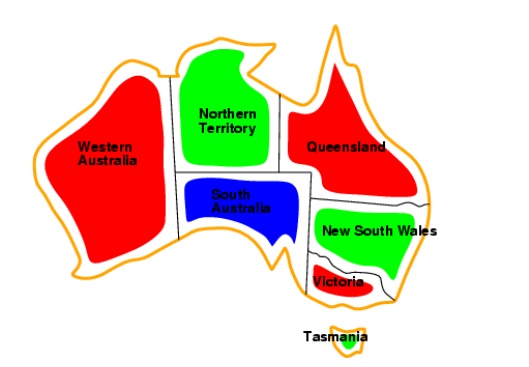
• Solutions are complete and consistent assignments, e.g., WA = red, NT = green,Q = red,NSW= green,V = red,SA = blue,T = green

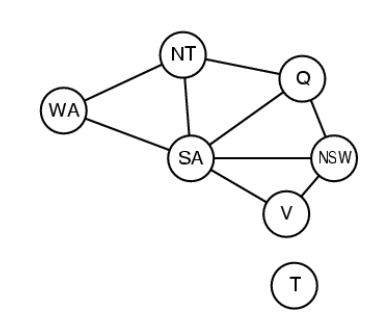
Constraint graph

•                      Binary CSP: each constraint relates two variables

•                      Constraint graph: nodes are variables, arcs are constraints

Varieties of CSPs

•                     Discrete variables

–  finite domains:

•                                                                     n variables, domain size d -O(dⁿ) complete assignments

•                                                                     e.g., Boolean CSPs, incl.~Boolean satisfiability (NP-complete)

–  infinite domains:

•                                                                     integers, strings, etc.

•                                                                     e.g., job scheduling, variables are start/end days for each job

•                                                                     need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3

•                                                                     Continuous variables

–  e.g., start/end times for Hubble Space Telescope observations

–  linear constraints solvable in polynomial time by linear programming

Varieties of constraints:

•                     Unary constraints involve a single variable,

–  e.g., SA ≠ green

•                     Binary constraints involve pairs of variables,

–  e.g., SA ≠ WA

–  Higher-order constraints involve 3 or more variables,

–  e.g., cryptarithmetic column constraints