Bragg's Equation and spectrometer method

X-RAYS AND CRYSTAL STRUCTURE

X-rays are electromagnetic waves of very short wavelength. The wave nature  of X-rays is not confirmed by diffraction experiment, because a grating of about 40 million ruling per cm is required for diffraction experiment. The preparation of such a grating is highly impossible. At the same time, crystallographers believed that atoms in crystals are regularly arranged with an interatomic distance of about 10-8 cm. The wavelength of X-rays is, also, in the order of 10-8 cm. Based on this, Laue suggested that crystal can be used as a three dimensional diffraction grating for X-rays. This suggestion is carried out successfully by Laue in his experiment using zinc sulphide crystal. The photograph obtained is known as Laue diffraction pattern.

The Laue experiment confirmed the wave nature of X-rays and also established the fact that atoms or ions in crystals are arranged in regular three dimensional lattice. Though Laue diffraction pattern gives more information about the symmetry of crystals, the interpretation of the pattern seems to be difficult.

Bragg's Equation

W.L.Bragg and W.H.Bragg derived a mathematical relation to determine interatomic distances from X-ray diffraction patterns. The scattering of X-rays by crystals could be considered as reflection from successive planes of atoms in the crystals. However, unlike reflection of ordinary light, the reflection of X-rays can take place only at certain angles which are determined by the wavelength of the X-rays and the distance between the planes in the crystal. The fundamental equation which gives a simple relation between the wavelength of the X-rays, the interplanar distance in the crystal and the angle of reflection, is known as Bragg's equation.

Bragg's equation is nl = 2d sinq

where n       is the order of reflection

l is the wavelength of X-rays

d is the interplanar distance in the crystal

q is the angle of reflection

Significance of Bragg's equation

1)    If we use X-rays of known wavelength (l), then the interatomic distance  (d) in an unknown crystal can be calculated. On the other hand, if we use a crystal whose interatomic distance 'd' is known, then the wavelength of

X-rays can be calculated.

2. The Bragg's equation gives the essential condition for diffraction to occur.

3. When the experiment is done, there will be a maximum reflection at a

particular angle q. That angle is noted. It corresponds to first order reflection  (n=1). If the angle 'q' is increased, maximum reflection occurs at some  other higher angle. It corresponds to second order reflection (n=2). Similarly,  third, fourth and higher order of reflection occur at certain specific angles. The values of angles obtained are in accordance with the Bragg's equation. Hence Bragg's equation is experimentally verified.

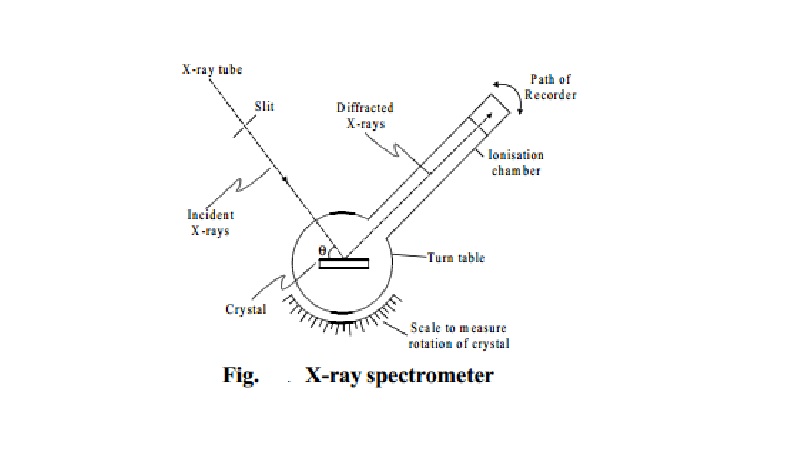
Bragg's spectrometer method

This method is one of the important method for studying crystals using X-rays. The apparatus consists of a X-ray tube from which a narrow beam of X-rays is allowed to fall on the crystal mounted on a rotating table.The rotating table is provided with scale and vernier, from which the angle of incidence, q can be measured.

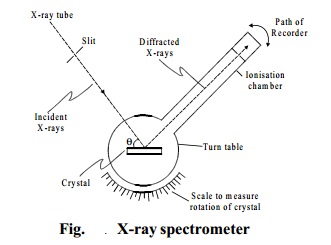
An arm which is rotating about the same axis as the crystal table, carries an ionisation chamber. The rays reflected from the crystal enter into the ionisation chamber and ionise the gas present inside. Due to the ionisation, current is produced which is measured by electrometer. The current of ionisation is a direct measure of intensity of reflected beam from the crystal. For different angles of incidence, the corresponding ionisation current is measured from the electrometer. These values are plotted in the form of graph.

For sodium chloride, the maximum reflection or peaks for 100 plane occurred  at q = 5.9 o , 11.85 o and 18.15 o . The sines of these angles are 0.103, 0.205 and 0.312 which are in the ratio 1:2:3. These peaks represent the first,second and third order reflections. The ratio confirms the correctness of Bragg's equation.