Artificial Intelligence: Grammars and Languages

Grammars and Languages

The types of grammars that exist are Noam Chomsky invented a hierarchy of grammars.

The hierarchy consists of four main types of grammars.

The simplest grammars are used to define regular languages.

A regular language is one that can be described or understood by a finite state automaton. Such languages are very simplistic and allow sentences such as “aaaaabbbbbb.” Recall that a finite state automaton consists of a finite number of states, and rules that define how the automaton can transition from one state to another.

A finite state automaton could be designed that defined the language that consisted of a string of one or more occurrences of the letter a. Hence, the following strings would be valid strings in this language:

aaa

a

aaaaaaaaaaaaaaaaa

Regular languages are of interest to computer scientists, but are not of great interest to the field of natural language processing because they are not powerful enough to represent even simple formal languages, let alone the more complex natural languages.

Sentences defined by a regular grammar are often known as regular expressions. The grammar that we defined above using rewrite rules is a context-free grammar.

It is context free because it defines the grammar simply in terms of which word types can go together—it does not specify the way that words should agree with each.

A stale dog climbs Mount Rushmore.

It also, allows the following sentence, which is not grammatically correct:

Chickens eats.

A context-free grammar can have only at most one terminal symbol on the right-hand side of its rewrite rules.

Rewrite rules for a context-sensitive grammar, in contrast, can have more than one terminal symbol on the right-hand side. This enables the grammar to specify number, case, tense, and gender agreement.

Each context-sensitive rewrite rule must have at least as many symbols on the right-hand side as it does on the left-hand side.

Rewrite rules for context-sensitive grammars have the following form:

A X B→A Y B

which means that in the context of A and B, X can be rewritten as Y.

Each of A, B, X, and Y can be either a terminal or a nonterminal symbol.

Context-sensitive grammars are most usually used for natural language processing because they are powerful enough to define the kinds of grammars that natural languages use. Unfortunately, they tend to involve a much larger number of rules and are a much less natural way to describe language, making them harder for human developers to design than context free grammars.

The final class of grammars in Chomsky’s hierarchy consists of recursively enumerable grammars (also known as unrestricted grammars).

A recursively enumerable grammar can define any language and has no restrictions on the structure of its rewrite rules. Such grammars are of interest to computer scientists but are not of great use in the study of natural language processing.

Parsing: Syntactic Analysis

As we have seen, morphologic analysis can be used to determine to which part of speech each word in a sentence belongs. We will now examine how this information is used to determine the syntactic structure of a sentence.

This process, in which we convert a sentence into a tree that represents the sentence’s syntactic structure, is known as parsing.

Parsing a sentence tells us whether it is a valid sentence, as defined by our grammar

If a sentence is not a valid sentence, then it cannot be parsed. Parsing a sentence involves producing a tree, such as that shown in Fig 10.1, which shows the parse tree for the following sentence:

The black cat crossed the road.

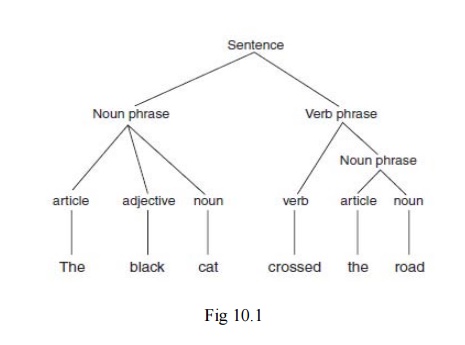
This tree shows how the sentence is made up of a noun phrase and a verb phrase.

The noun phrase consists of an article, an adjective, and a noun. The verb phrase consists of a verb and a further noun phrase, which in turn consists of an article and a noun.

Parse trees can be built in a bottom-up fashion or in a top-down fashion.

Building a parse tree from the top down involves starting from a sentence and determining which of the possible rewrites for Sentence can be applied to the sentence that is being parsed. Hence, in this case, Sentence would be rewritten using the following rule:

Sentence→NounPhrase VerbPhrase

Then the verb phrase and noun phrase would be broken down recursively in the same way, until only terminal symbols were left.

When a parse tree is built from the top down, it is known as a derivation tree.

To build a parse tree from the bottom up, the terminal symbols of the sentence are first replaced by their corresponding nonterminals (e.g., cat is replaced by noun), and then these nonterminals are combined to match the right-hand sides of rewrite rules.

For example, the and road would be combined using the following rewrite rule: NounPhrase→Article Noun