Chapter: 11th 12th std standard Class Organic Inorganic Physical Chemistry Higher secondary school College Notes
Vanderwaal's Equation of state : Units, Significance, Limitations
Vanderwaal's Equation of state
For an ideal gas PV = nRT, is considered as the
equation of state. By including the correction terms in the ideal gas equation
to account for
(i) volume
of the gaseous molecules themselves in V and (ii) the intermolecular forces of
attraction in pressure, P, the equation of state for the real gas is arrived,
J.O Vanderwaal's deduced the equation of state of real gases.
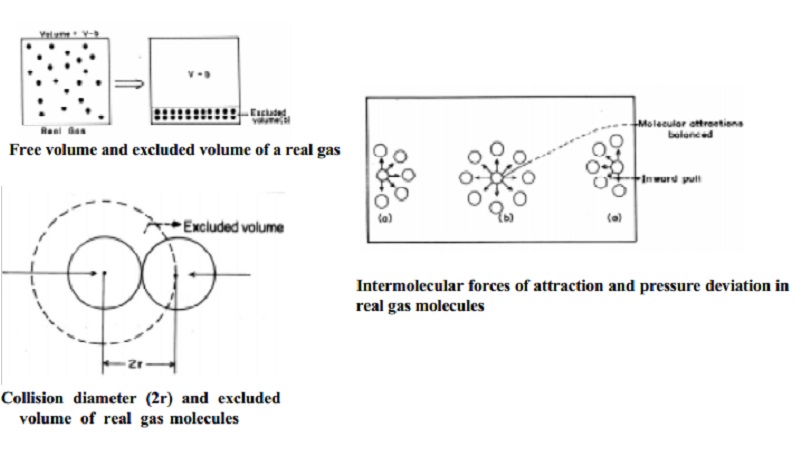
i) Volume correction of
real gas
The volume
of a gas is the free space in the container in which molecules move about.
Volume V of an ideal gas is the same as the volume of the container. The volume
of a real gas is, therefore, ideal volume minus the volume occupied by the gas
molecules themselves. If Vm is the volume of the single molecule
then, the excluded volume which is termed as "b" is determined as
follows.
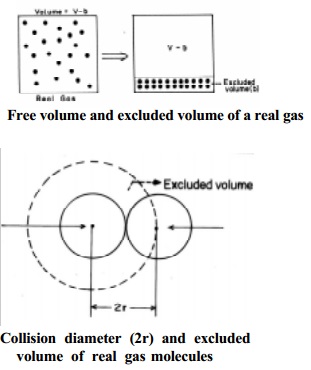
Let us consider two colliding molecules with radius `r'. The space
indicated by dotted sphere of radius 2r will not be available for other
molecules to freely move about. (i.e) the dotted spherical volume is known as excluded volume per pair of the
molecules.
Thus,
excluded
volume for two molecules = 4/3 x pi (2r) 3
=8( 4/3 pi
r 3 )
Excluded
volume per molecule
VC = ½ x 8 x 4/3 x pi r 3
= 4 Vm
where Vm
is the actual volume of a single molecule.
The
excluded volume for n molecules, 'b' = 4n Vm, where 4 Vm is the excluded volume of a molecule.
The corrected volume of the real gas is = (V-b) = free space for molecular movement.
ii) Pressure Correction
In a real
gas the pressure deviation is caused by the intermolecular forces of
attraction. According to kinetic theory, the pressure of the gas is directly
proportional to forces of bombardment of the molecules on the walls of the
container. Consider a molecule placed in the interior of the container. It is
surrounded equally by other gas molecules in all directions such that the
forces of attraction in any direction is cancelled (or) nullified by similar
force operating in the opposite direction. However a molecule near the wall of
the container which is about to strike is surrounded unequally by other gaseous
molecules as shown in Fig.
The molecule near the wall experiences attractive forces only such that
it will strike the wall with a lower force which will exert a lower pressure
than if such attractive forces are not operating on it. Therefore it is
necessary to add the pressure correction term to the pressure of the gas to get
the ideal pressure. The corrected pressure should be P + p' where p' is the
pressure correction factor.

The force
of attraction experienced by a molecule near the wall depends upon the number
of molecules per unit volume of the bulk of the gas. It is found experimentally
that, p' is directly proportional to the square of the density of the gas (r) which is a measure of the intermolecular
attraction of the molecules.
P¢ = p2
Density is
inversely related to the volume `V' which is the volume occupied by one mole of
the gas. Therefore P¢ of one
mole of the gas is given by
P¢ = 1/ V2
where `a' is a proportionality constant that depends upon the nature of
the gas.
corrected pressure = P + P¢
= P + (a/ V2)
Replacing the term for corrected volume and the corrected pressure in
the ideal gas equation for one mole, the equation of state of the real gas is
( P + (a/ V2) ) + (
V-b ) = RT
where `a' and `b' are known as vanderwaal's constants.
This equation is also known as Vanderwaal's equation of state.
If there are `n' moles of the real gas then the vanderwall's equation
becomes
P + (n2a / V2) = (V-nb) = nRT
Units for vanderwaal's
constant
The dimensions of the vanderwaal's constant a and b depend upon the
units of P and V respectively.
a= Pressure . (Volume)2 / mole2
a = atm . dm6 mol-2 (_ 1 litre = 1 dm3)
Thus a is expressed as atm.dm6 mol-2 units. If
volume is expressed in dm3 then b is expressed as
Vo1/n = dm3/mol
V/ n =dm3mol-1
Unit of b = dm3mol-1
Significance of
Vanderwaal's constant (a) and (b)
1.
The term a/V2 is the measure of the
attractive forces of the molecules. It is also called as the cohesion pressure
(or) internal pressure.
2.
The inversion temperature of a gas can be
expressed in terms of `a' and `b'
Ti= 2a / Rb
3.
The vanderwaal constants `a' and `b' enable the
calculation of critical constants of a gas.
Limitations of
Vanderwaal's equation
1.
It could not explain the quantitative aspect of
deviation satisfactorily as it could explain the qualitative aspects of P and V
deviations.
2.
The values of `a' and `b' are also found to vary
with P and T, and such variations are not considered in the derivation of
Vanderwaal equation.
3.
Critical constants calculated from Vanderwaal's
equation deviate from the original values determined by other experiments.
Related Topics