Gaseous state - Critical phenomena

Critical phenomena

The essential condition for the liquefaction of the gas is described by the study of critical temperature, critical pressure and critical volume and their inter relationships.

When a gaseous system is transformed to its liquid state, there is a tremendous decrease in the volume. This decrease in volume can be effectively brought about by lowering of temperature, or by increasing pressure (or) by both. In both these effects the gaseous molecules come closer to each other and experience an increase in force of attraction which results in liquefaction of gases. At any constant temperature when pressure is increased volume is decreased and vice versa. Such P-V curves at constant temperature are known as isotherms. A typical isotherm can be considered similar to Fig.9.2.

The figure 9.2 shows the continuous decrease in pressure with increase in volume for both ideal and real gases. There is a definite deviation exhibited by the real gas from ideal gas behaviour at high pressure and low volumes.

Critical temperature (Tc)

It is defined as the characteristic temperature of a gas at which increase in pressure brings in liquefaction of gas above which no liquefaction occurs although the pressure may be increased many fold. For instance T_c of CO₂ is 31.1 o C. This means that it is not possible to liquefy CO2 by applying pressure when its temperature is above 31.1 o C.

Critical pressure (Pc)

It is defined as the minimum pressure required to liquefy 1 mole of a gas present at its critical temperature.

Critical volume (V_c)

The volume occupied by 1 mole of a gas at its critical pressure and at critical temperature is the critical volume (Vc) of the gas.

A gas is said to be at its critical state when its pressure, volume and temperature are Pc, Vc and Tc.

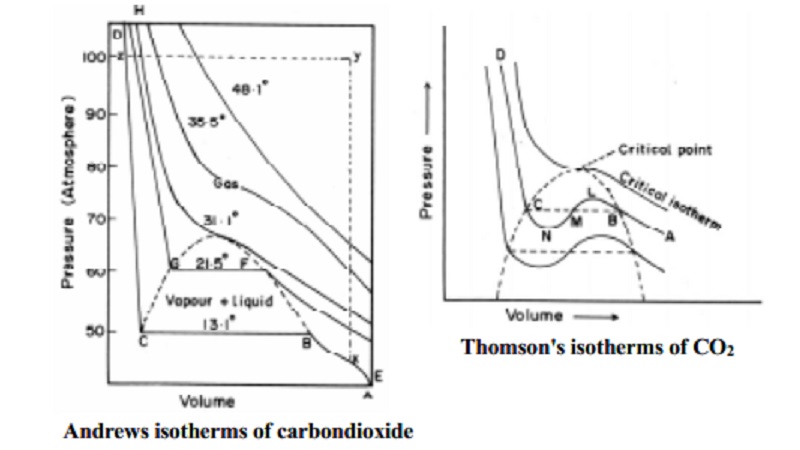
1)Andrews isotherms of carbondioxide

The importance of critical temperature of a gas was first discovered by Andrews in his experiments on pressure - volume isotherms of carbon dioxide gas at a series of temperature. The isotherm of carbondioxide determined by him at different temperatures are shown in Fig.

Consider first the isotherm at the temperature 13.1 o C. The point A represents carbondioxide in the gaseous state occupying a certain volume under a certain pressure. On increasing the pressure its volume diminishes as is indicated by the curve AB. At B, liquefaction of gas commences and thereafter a rapid decrease in the volume takes place at the same pressure, since more and more of the gas is converted into the liquid state. At C, the gas becomes completely liquefied. After `C' the increase of pressure produces only a very small decrease in volume. This is shown by a steep line CD which is almost vertical. Thus, along the curve AB, carbon dioxide exist as gas. Along BC, it exists in equilibrium between gaseous and liquid state. Along CD it exists entirely as a liquid. The isotherm at 21.5 o C shows that the decrease in volume becomes smaller because higher the temperature greater is the volume. Therefore more pressure is applied to decrease the volume. This effect makes liquefaction to commence at higher pressure compared to the previous isotherm at 13.1 o C.

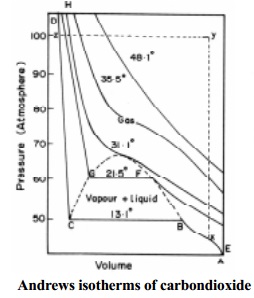
At still higher temperature, the horizontal portion of the curve becomes shorter and shorter until at 31.1 o C it reduces to a point. The temperature 31.1 o C is regarded as the critical temperature of CO2. At this temperature, the gas passes into liquid imperceptibly. Above 31.1 o C the isotherm is continuous. CO2 cannot be liquefied above 31.1 o C no matter how high the pressure may be. The portion of area covered by curve H with zyx portion always represents the gaseous state of CO2.

2) Continuity of state

Thomson's experiment

Thomson (1871) studied the isotherm of CO₂ drawn by Andrews. He suggested that there should be no sharp points in the isotherms below the critical temperature. These isotherms should really exhibit a complete continuity of state from gas to liquid. This, he showed as a theoretical wavy curve. The curve MLB in Fig.9.7 represents a gas compressed in a way that it would remain stable. The curve MNC represents a superheated liquid because compression above Tc, leads to heating effects. This type of continuity of state is predicted by Vanderwaal's equation of state which is algebraically a cubic equation. The Vanderwaal's equation may be written as

PV³ - (RT + Pb) V² + aV - ab = 0

Thus, for any given values of P and T there should be three values of V. These values are indicated by points B,M and C of the wavy curve. The three values of V become closer as the horizontal part of the isotherm rises. At the critical point the three roots of Vanderwaal 'V' become identical and there is no longer any distinction between the gas and liquid states. Here, the gas is said to be in critical state. This effect enables the calculation of Tc, Pc and Vc in terms of Vanderwaal's constants.

3) Derivation of critical constants from Vanderwaal's constants

Let us derive the values of critical constants T_c (critical temperature), V_c (critical volume) and P_c (critical pressure) in terms of the Vanderwaal's constants `a' and `b'. The Vanderwaal's equation is given by

T_c =8a / 27Rb

Hence the critical constants can be calculated using the values of Vanderwaal's constants of a gas and vice versa. Since P_c and T_c can often be determined experimentally, these values may be employed to calculate the constants a and b.

a  =  3Vc² Pc

b = Vc /3

Based on the critical temperature values, gases are categorised as "permanent" and "temporary" gases. H₂, N₂, He, .... gases having very low critical temperature belong to the permanent type. Gases like NH₃, CO₂, SO₂, HCl etc. having critical temperature in the ordinary range of temperatures belong to the temporary gases type.