Chapter: Civil : Structural dynamics of earthquake engineering
Free vibration of single degree of freedom systems (undamped) in relation to structural dynamics during earthquakes
Free
vibration of single-degree-of-freedom systems (undamped) in relation to
structural dynamics during earthquakes
Abstract: In this
chapter, the governing equations of motion are formulated for free
vibration of single-degree-of-freedom (SDOF) (undamped) system. Vibration
characteristics are studied by taking an example of a simple pendulum. Free
vibration of rigid bodies without damping is also discussed.
Key words: frequency,
amplitude, phase angle, harmonic motion, Newton├Ģs law, Rayleigh method.
Introduction
The study of vibration
deals with oscillatory motion of a machine or a structure about an equilibrium
position when it is subjected to shock or an oscillating force. The
oscillations may be repeated uniformly, or change with time. Vibration in
machines and structures is quite common and undesirable. In most cases its
undesirable effects may be classified with respect to human characteristics and
damage to engineering structures. An extreme example is a slender skyscraper
whose wind-induced oscillations are entirely safe for the structure, yet
unpleasant to the occupants of the upper floors. At the other extreme, certain
vibrations in aeroplanes may be unnoticeable to the passengers, yet cause
damage (fatigue) with catastrophic consequences.
The simultaneous occurrence of unpleasant and
structurally damaging vibrations such as those in cars and trucks is the most
common. Some vibrations are desirable, viz. beating of the heart, planets
revolving around the sun and the consolidation of concrete by using vibrators.
Damage to the structure occurs through earthquake loadings by forming cracks
due to undesirable vibrations. Hence, in such cases, vibrations must be reduced
to the minimum or should be eliminated. For elimination or reduction and to
produce controlled vibrations, where necessary, a study of basic vibration
theory is essential.
Formulation of the equation
of motion
The governing equation of motion can be formulated using
ŌĆó
simple harmonic motion theory;
ŌĆó
Newton's second law;
ŌĆó
Energy method;
ŌĆó
Raleigh method;
ŌĆó
D├ĢAlembert├Ģs principle.
Simple harmonic theory
A special kind of motion occurs when the force on
the body is proportional to the displacement of the body from equilibrium as
shown in Fig. 2.1. If this force acts towards the equilibrium position of the
body, a repetitive back and forth motion about this position occurs. Such a
motion is an example of periodic or oscillatory motion. F is
proportional to (-x).

where Žēn is known as natural frequency.
The particle moving along x-axis is said to exhibit simple harmonic
motion if it satisfies Eq. 2.8, where A, Žēn and Žå are constants of the motion. In
order to give a physical meaning to these constants, the graph in Fig. 2.2
shows x as a function of time t.


2.1 Motion of the particle when
force is proportional to the displacement.
The constant A is called amplitude
of the motion, which is the maximum displacement of the particle in either a
positive or negative x-direction. The constant angle Žå is called the phase constant
(or phase angle) acting along with the amplitude A which can be
determined uniquely by the initial displacement and initial velocity of the
particle.
Note: The
function x is periodic and repeats itself when Žēnt increases
by 2ŽĆ rad.
The period T of the motion is the time it takes for the particle to com
plete one full cycle, i.e.
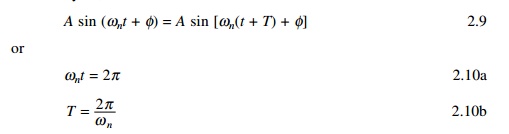
The inverse of the period is called frequency
(f) of the motion. It represents the number of oscillations that a
particle makes per unit time.

From Eq. 2.13, we get the maximum displacement,
velocity and acceleration as:
xmax =
A 2.14a
vmax = ŽēnA 2.14b
amax = Žē n2 A 2.14c
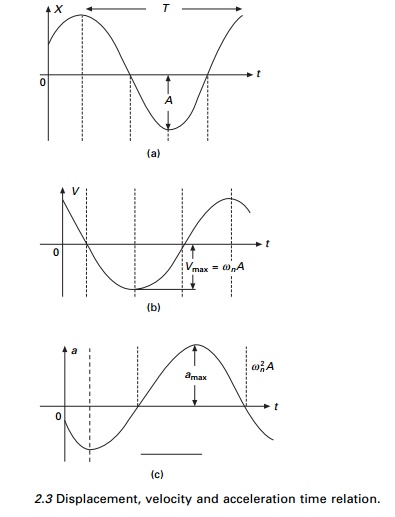
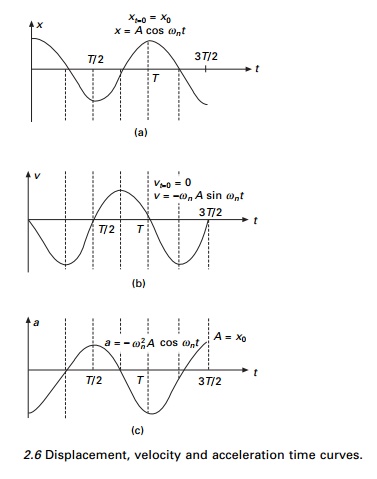
Figure 2.3 shows displacement vs. time, velocity
vs. time and acceleration vs. time curves. The curves shown in Fig. 2.3
indicate that the phase difference between the velocity and displacement is ŽĆ/2 radians or 90┬ o , i.e. when x is maximum or minimum, the velocity is
zero. Likewise, when x is zero the velocity is maximum. Furthermore, the
phase of the acceleration is out of phase by ŽĆ radians or 180┬ o with
displacement, i.e. when x is maximum, acceleration is maximum in the
opposite direction.
Equation 2.3 is a second order differential
equation and therefore two initial conditions are required to solve the
equation. Let x t = 0 = x 0 ; v t
=0 be the
initial conditions. Substituting t = 0 in Eq. 2.13,
x0 = A sin
Žå
v0 = + Žēn A cos Žå 2.15a
a0 = Ōł'Žē n2 A sin Žå 2.15b
From Eq. 2.15a and 2.15b, we get 2.15c
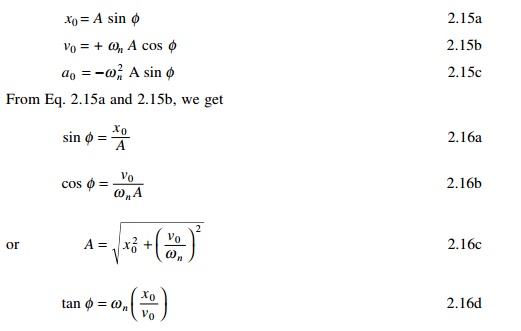
Thus we see that Žå and A can be calculated
if x 0 ,Žē n
and v0 are known. The following important properties are to
be noted if a particle is moving
in simple harmonic motion.
┬Ģ The
displacement, velocity and acceleration shown in Fig. 2.3 vary sinusoidally
with time but are not in phase.
’éĢ The acceleration of
the particle is proportional to the displacement but in the opposite direction.
┬Ģ The frequency and period
of motion are independent of amplitude.
In this book, we use force unit
of newton, length unit of metres and mass unit of kilogram.
Example 2.1
A body oscillates with a simple
harmonic motion along the x-axis. Its displacement varies with time
according to x = 8 cos (ŽĆt + ŽĆ/4), where t is in seconds
and the angle is in radians.
(a) Determine
the amplitude, frequency and period of motion.
Calculate the velocity and acceleration of the
body at any time t.
(c) Using the
results of (b), determine the position, velocity and acceleration of the body
at t = 1 second.
(d) Determine
the maximum speed and acceleration.
(e) Find the
displacement of the body between t = 0 to t = 1 second.
Solution
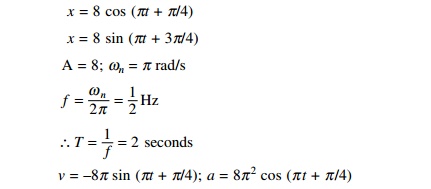
At t = 1
x = 8 cos (ŽĆ + ŽĆ/4) = 8 cos (5ŽĆ/4) = ├É5.66 m
v = ├É8ŽĆ sin (5ŽĆ/4) = 17.78 m/s2
a = ├É8ŽĆ2 cos (ŽĆ + ŽĆ/4) = 55.8 m/s2
vmax = 8ŽĆ m/s, amax
= 8ŽĆ 2 m/s2
At t = 0
x0 = 8 cos
(0 + ŽĆ/4) =
5.66 m
At t = 1 s
x = -2.83 ├- 2 = -5.66 m
Hence displacement from t = 0 to t = 1 second is
Ōłåx = x -
x0 = -5.66 - 5.66 = -11.32 m
Since the particle's velocity
changes sign during the first second, the magnitude of Ōłåx is not
the same as the distance travelled in the first second.
NewtonŌĆÖs second law
SpringŌĆ'mass system
Consider a physical system consisting of mass
attached to the end of a spring as shown in Fig. 2.4 where it is free to move.
Due to the self-weight of the mass, the spring elongates by x0
and this position is called the equilibrium position. Considering the free body
diagram
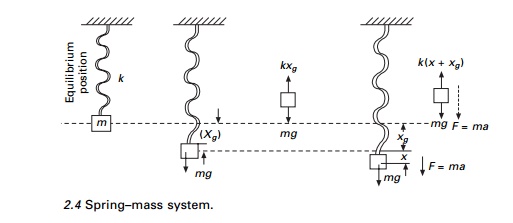
kxg = mg 2.17
Assume that the spring oscillates back and forth
when it is disturbed from equilibrium position. From Newton's second law,
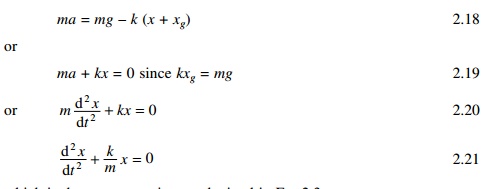
which is the same equation as obtained in Eq. 2.3
We see that the solution must be that of simple
harmonic motion. Wherever the force acting on a particle is linearly
proportional to the displacement and acts in the opposite direction, the
particle is said to be in simple harmonic motion.
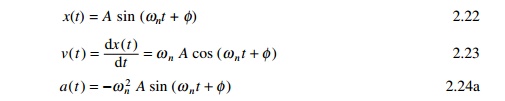
In Eq. 2.18, self-weight is cancelled with kxg
and usually it is not considered during the analysis. Since period T = 2ŽĆ/Žēn and
frequency is inversely proportional to period, we can express the period and
frequency of the system as

2.6 Displacement, velocity and
acceleration time curves.
Case II
Suppose if the mass is given an initial velocity v0
in the downward direction from the equilibrium position so that at t =
0, v = v0 and x0 = 0 at t =
0, we get
Example 2.2
A car of mass 1300 kg is
constructed using a frame supported by four springs. Each spring has a force
constant 20 000 N/m. If the combined mass of two people in a car is 160 kg,
find the frequency of vibration when it is driven over a pothole on the road.
Also determine the period of execution of two complete vibrations.
Solution
From angular frequency,
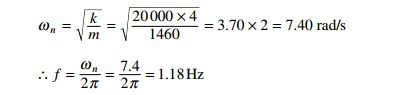
Period of vibration T = 1/f
= 0.847 seconds. Time for one complete vibration = 0.847 seconds.
Ōł┤ Time
taken for two complete vibrations = 1.694 seconds.
Example 2.3
A mass of 400 g shown in Fig. 2.7 is connected to
a light spring whose force constant is 5 kN/m. It is free to oscillate on a
horizontal frictionless track. If the mass is displaced 10 cm from equilibrium
and released from rest, find (a) period of motion, (b) maximum speed of the
mass, (c) maximum acceleration of the mass, and (d) equations for displacement,
speed and acceleration as function of time.

(d) Equations as a function of time
x = A cos Žē n t = 0.1 cos 3.53 t
v = ├ÉŽēnA sin Žēnt = ├É3.53
├- 0.1 sin
(3.53t) = Ð 0.353 sin (3.53t)
a = Ōł'Žē n2 A cos Žē n t = Ōł'1.246 cos
3.53t
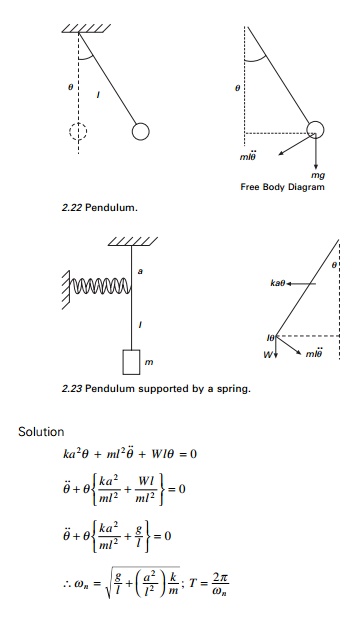
Simple pendulum
The simple pendulum is another mechanical system
that moves in an oscillatory motion. It consists of a point mass 'm'
suspended by means of light inextensible string of length L from a fixed
support as shown in Fig. 2.8. The motion occurs in a vertical plane and is
driven by a gravitational force. The forces which are acting on the mass are
shown in the figure. The tangential component of the gravitational force, mg
sin ╬Ė, always acts towards the mean
position ╬Ė = 0
opposite to the displacement, restoring force acting tangent to the arc.

For small displacement sin ╬Ė == ╬Ė and the
motion of the bob is along the arc
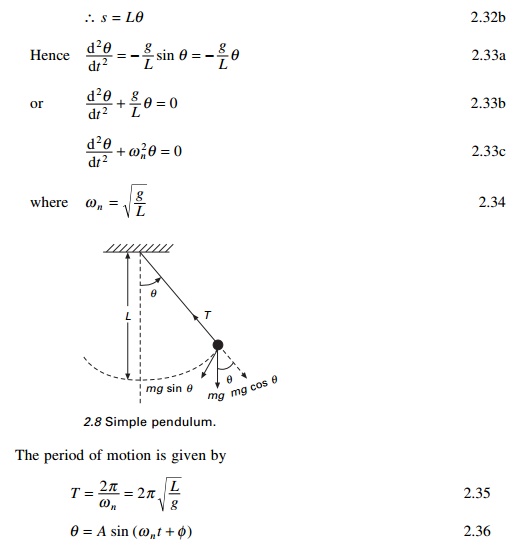
From the above equation, it is
seen that the period and frequency of a simple pendulum depend only on the
length of the string and the value g.
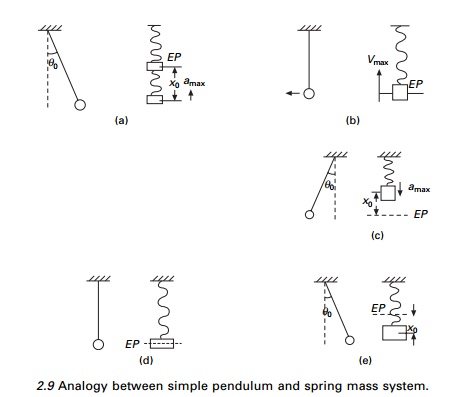
Since the period is independent
of the mass, a pendulum of equal length at the same location oscillates with
equal periods. The analogy between the simple pendulum is the massÐspring
system as shown in Fig. 2.9. The displacement, velocity, acceleration, kinetic
energy and potential energy are given in Table 2.1 for various positions of the
pendulum.
Example 2.4
A man wants to measure the height of a tower. He
notes that a long pendulum extends from the ceiling almost to the floor and
that its period is 24 s. Determine (a) the height of the tower and (b) the
period when the pendulum is taken to the moon where g = 1.67 m/s2.

2.6 Comparison of simple harmonic motion and
uniform circular motion
Consider a particle at a point P moving in a
circle of radius A with constant angular speed Žēn as shown
in Fig. 2.10. We refer to the circle as reference
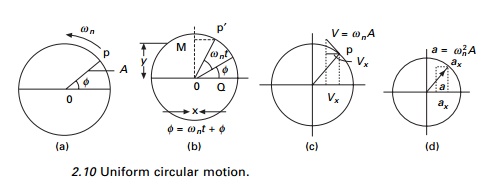
circle. As the particle rotates
its position, the vector rotates about the origin 0 and at t = 0, 0P
makes an angle of Žå. At time
t, ╬Ė = Žēnt + Žå.
This expression shows that point M
moves with simple harmonic motion along the y-axis. Therefore we
conclude that:
Simple harmonic motion along a
straight line can be represented by the projection of uniform circular motion
along diameter of a reference circle.
Similarly, we can show that point
╬Ė exhibits simple harmonic motion.
Therefore:
Uniform circular motion can be
considered as a combination of two simple harmonic motions.
Energy method
Energy of simple harmonic
oscillator
Consider a massÐspring system discussed in Section
2.3 (see Fig. 2.4). Assuming the system to be conservative, we expect the total
mechanical energy as constant. We can express kinetic energy as
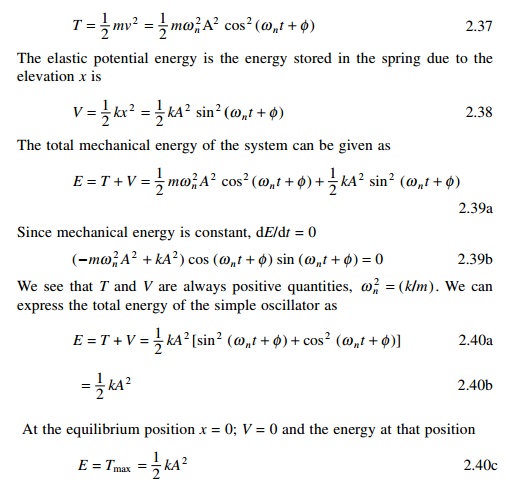
Plots of kinetic and potential
energy versus time are shown in Fig. 2.11a for Žå = 0. The variations of T
and V with displacements are plotted in Fig. 2.11b. Energy is
continuously being transformed between potential energy stored in the spring
and the kinetic energy of the mass. The kinetic energy and potential energy for
the pendulum and spring mass system are shown in Fig. 2.9.
Example 2.5
A mass 0.5 kg is connected to a
light spring of stiffness 20N/m, and oscillates on a horizontal frictionless
track.
(a) Calculate
the total energy of the system and the maximum speed of the mass if the
amplitude of motion is 3cm.
(b) Calculate
the velocity of the mass when the displacement is equal to 2 cm.
(c) Compute
kinetic and potential energies of the system when the displacement is equal to
2cm.

Rayleigh method
E = V
+ T = VMAX
= TMAX 2.41a
When strain energy is maximum,
kinetic energy is zero and vice versa. From Eq. 2.37 and 2.38

DŌĆÖAlembertŌĆÖs
principle
DŌĆÖAlembert├Ģs principle of dynamic
equilibrium is a convenient method for establishing the equation of motion for
simple single-degree-of-freedom (SDOF) and multiple-degree-of-freedom (MDOF)
systems. It essentially involves invoking NewtonŌĆÖs second law of motion to the
system.
Considering Eq. 2.20, introduce
the appropriate inertia force and it can be reasoned that applied force on the
mass is in equilibrium with inertia force, i.e. inertia force is acting in the
opposite direction to the applied force. Therefore dynamic problem is reduced
to equivalent static problem.
D AlembertŌĆÖs principle
states that a system may be set in a state of dynamic equilibrium by adding to
the external forces a fictitious force which is commonly known as the inertial.
Applying the equation of
equilibrium for the free body shown in Fig. 2.12 we get
Mx + kx =0 ----- -- 2.42
Free
vibration of rigid bodies without damping
The basic concepts
of analysing a vibrating system that were developed up to Section 2.6 are a
particular class of problem. The following list gives the characteristics of
problems and some practical considerations.
’éĢ One degree of freedom. A degree of freedom
is defined as the independent coordinate with which we define the displaced
shape of the structure. A system with a single coordinate function is said to
be a one-degree-of- freedom system.
’éĢ Free vibration. Equation 2.3 is valid when a
disturbing force is applied only once to give a mass on initial displacement.
The mass is in free vibration when only two kinds of forces are acting on it:
(a) an elastic- restoring force within the system and (b) gravitational or
other constant forces that cause no displacement from the equilibrium position
of the system.
’éĢ Undamped vibration. In the absence of
dissipative forces acting on a vibrating mass, the amplitude of vibration is
constant, and the motion is said to be undamped.
’éĢ Natural frequency. Each mass spring system
vibrates at a characteristic frequency in free vibration. This is known as
natural frequency of the system.
ŌĆó
Lumped parameters. Strictly
speaking, Eq. 2.3 is valid only for a particle of mass m and a
spring of no mass and spring constant k. In practice, the mass of a
translating rigid body is assumed to be concentrated as a particle and the mass
of the spring is completely ignored.
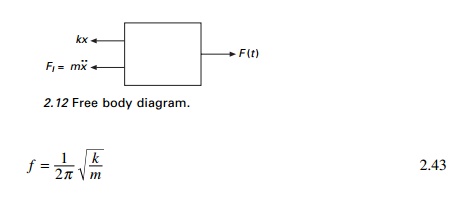
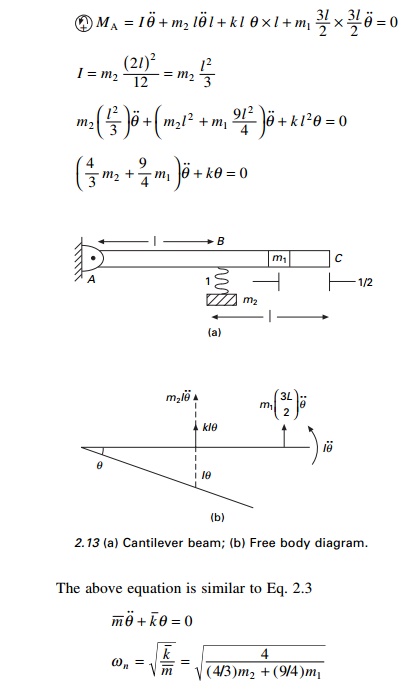
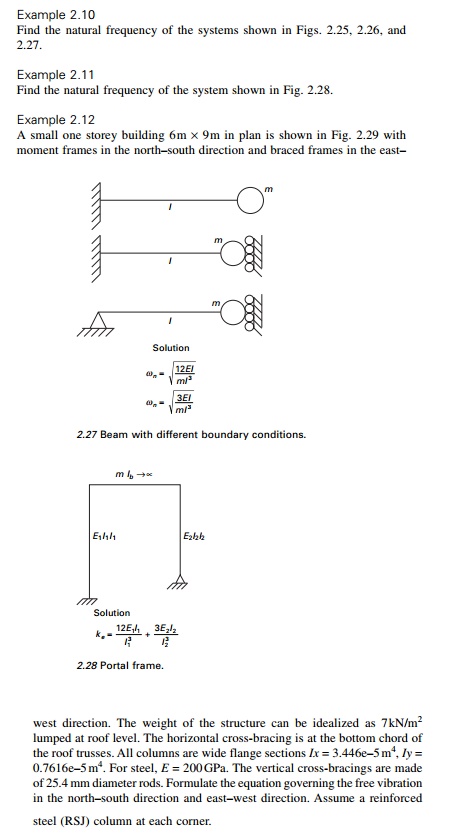
Example 2.6
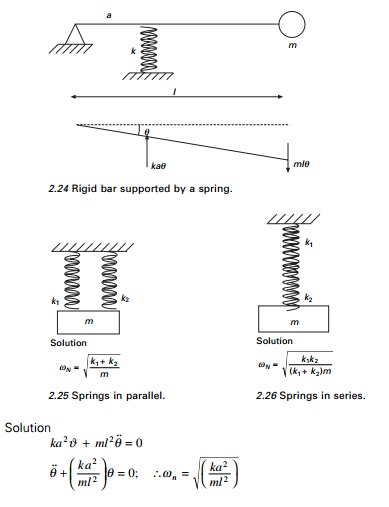
Find the natural frequency of the system shown in Fig. 2.13.
Solution
Taking moment at A
Example 2.7
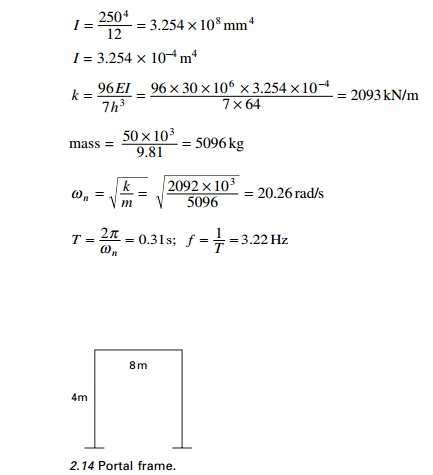
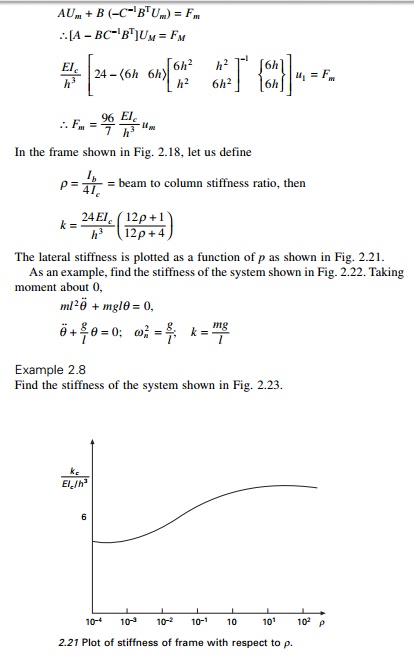
A single one storey reinforced
concrete (RC) building idealized as a massless frame is shown in Fig. 2.14
supporting a dead load of 50 kN at the roof level. The frame is 8 m wide and 4
m high. Each column and beam is 250 mm square. Assume Young├Ģs modulus of
concrete as 30 ├- 106 kN/m2
determine the natural frequency and period of the system. Assume stiffness of
an equivalent SDOF system is k = 96EI/7h3.
Solution
Moment of inertia of the
cross-section
Program 2.1: MATLAB
program to draw displacement, velocity and acceleration with respect to time
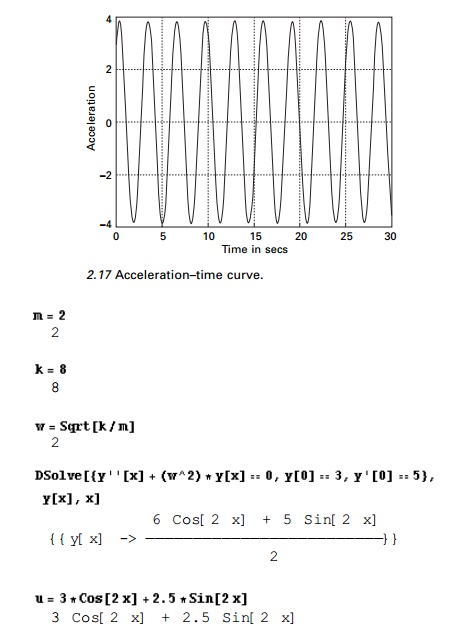
Consider the springÐmass system
shown in Fig. 2.4 with mass of 2kg m and stiffness of 8 N/m. We can write the
following MATLAB program to draw the displacementÐtime, velocityÐtime and
accelerationÐtime curves. We can solve symbolically the second order
differential equation as shown in the listing. Initial displacement and
velocity may be assumed as 3 m and 5 m/s.
1 Listing of
MATLAB program
clc; close all; m=2; k=8;
dt=0.02;
w=sqrt(k/m);
y=dsolve(├'D2y=-2^2*y├Ģ,├'y(0)=3├Ģ,├'Dy(0)=5├Ģ,├'x├Ģ); simplify(y)
for i=1:1500 t(i)=(i-1)*dt;
z(i)=3*cos(w*t(i))+5*sin(w*t(i))/w;
v(i)=-w*3*sin(w*t(i))+5*cos(w*t(i)); a(i)=-3*w^2*cos(w*t(i))-5*w*sin(w*t(i));
end figure(1)
plot(t,z,├'k├Ģ) xlabel(├'t├Ģ)
ylabel(├'u├Ģ)
title(├' Displacement Time Curve├Ģ)
figure(2)
plot(t,v,├'k├Ģ) xlabel(├'t├Ģ)
ylabel(├'v├Ģ)
title(├'Velocity time curve├Ģ)
figure(3)
plot(t,a,├'k├Ģ) xlabel(├'t├Ģ)
ylabel(├'a├Ģ)
title(├'Acceleration time curve├Ģ)
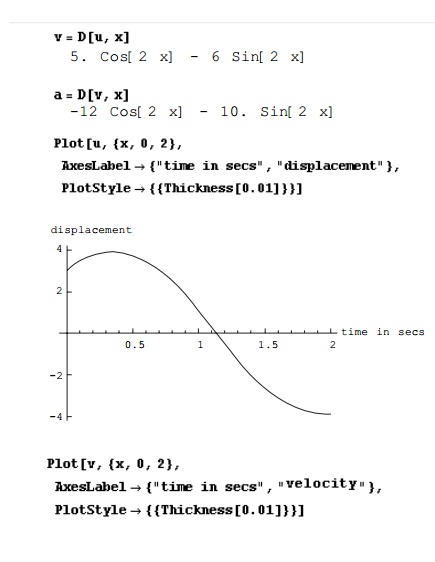
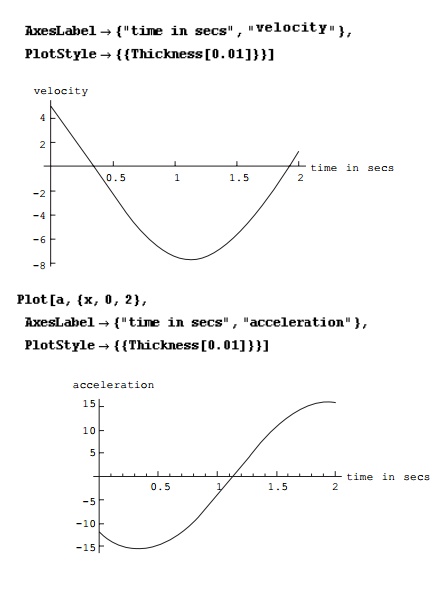
Figures 2.15, 2.16 and 2.17
represent displacementÐtime, velocityÐtime and accelerationÐtime curves.

Program 2.2: MATHEMATICA
program to draw displacement, velocity and acceleration with respect to time
2.12.1 Listing of MATHEMATICA program
The listing of the program in
MATHEMATICA is shown below. Using MATHEMATICA we can solve the second order
differential equation and plot the displacementÐtime, velocityÐtime and
accelerationÐtime curves.
Free vibration of
structural systems
1 Laterally loaded
elastic system
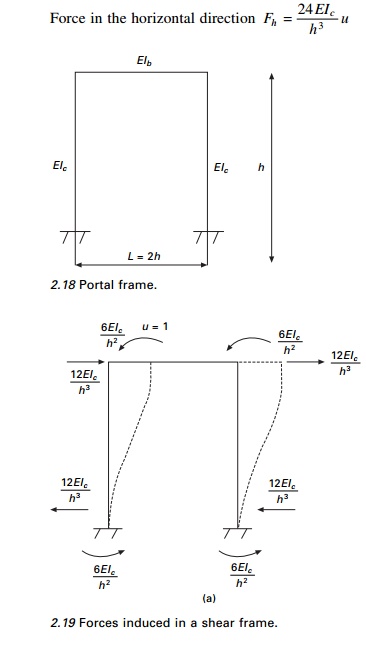
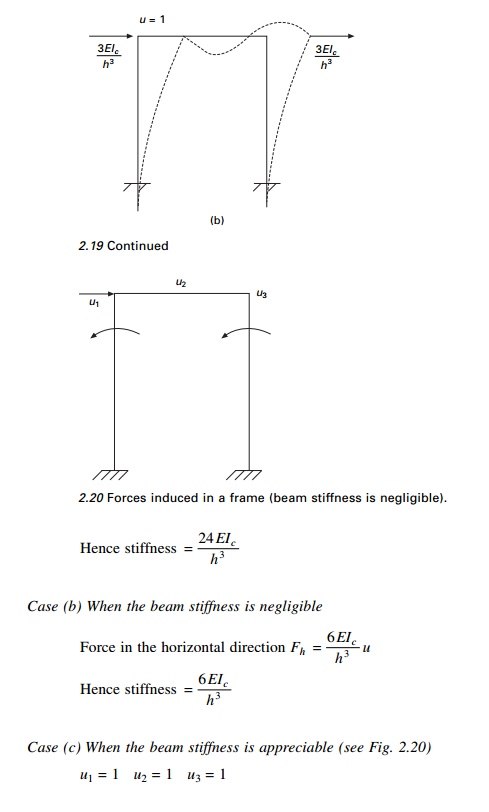
Consider the portal frame as shown in Fig. 2.18.
Case (a) When the beam stiffness is infinitely
rigid (shear frame)
From Fig. 2.19a:

Example 2.9
Find the natural frequency of the
system (Fig. 2.24) having mass less rigid rod

Related Topics