What Is an Algorithm?

What Is an Algorithm?

Although there is no universally agreed-on wording to describe this notion, there is general agreement about what the concept means:

An algorithm is a sequence of unambiguous instructions for solving a problem, i.e., for obtaining a required output for any legitimate input in a finite amount of time.

This definition can be illustrated by a simple diagram (Figure 1.1).

The reference to “instructions” in the definition implies that there is some-thing or someone capable of understanding and following the instructions given. We call this a “computer,” keeping in mind that before the electronic computer was invented, the word “computer” meant a human being involved in perform-ing numeric calculations. Nowadays, of course, “computers” are those ubiquitous electronic devices that have become indispensable in almost everything we do. Note, however, that although the majority of algorithms are indeed intended for eventual computer implementation, the notion of algorithm does not depend on such an assumption.

As examples illustrating the notion of the algorithm, we consider in this section three methods for solving the same problem: computing the greatest common divisor of two integers. These examples will help us to illustrate several important points:

The nonambiguity requirement for each step of an algorithm cannot be com-promised.

The range of inputs for which an algorithm works has to be specified carefully. The same algorithm can be represented in several different ways.

There may exist several algorithms for solving the same problem.

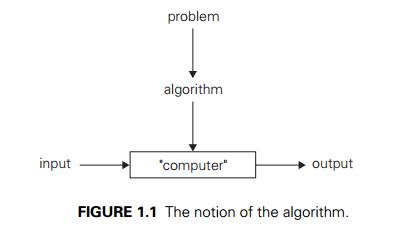
FIGURE 1.1 The notion of the algorithm.

Algorithms for the same problem can be based on very different ideas and can solve the problem with dramatically different speeds.

Recall that the greatest common divisor of two nonnegative, not-both-zero integers m and n, denoted gcd(m, n), is defined as the largest integer that divides both m and n evenly, i.e., with a remainder of zero. Euclid of Alexandria (third century B.C.) outlined an algorithm for solving this problem in one of the volumes of his Elements most famous for its systematic exposition of geometry. In modern terms, Euclid’s algorithm is based on applying repeatedly the equality

gcd(m, n) = gcd(n, m mod n),

where m mod n is the remainder of the division of m by n, until m mod n is equal to 0. Since gcd(m, 0) = m (why?), the last value of m is also the greatest common divisor of the initial m and n.

For example, gcd(60, 24) can be computed as follows:

gcd(60, 24) = gcd(24, 12) = gcd(12, 0) = 12.

(If you are not impressed by this algorithm, try finding the greatest common divisor of larger numbers, such as those in Problem 6 in this section’s exercises.)

Here is a more structured description of this algorithm:

Euclid’s algorithm for computing gcd(m, n)

Step 1 If n = 0, return the value of m as the answer and stop; otherwise, proceed to Step 2.

Step 2 Divide m by n and assign the value of the remainder to r.

Step 3 Assign the value of n to m and the value of r to n. Go to Step 1.

Alternatively, we can express the same algorithm in pseudocode:

ALGORITHM                 Euclid(m, n)

//Computes gcd(m, n) by Euclid’s algorithm

//Input: Two nonnegative, not-both-zero integers m and n //Output: Greatest common divisor of m and n

while n  = 0 do

r ← m mod n m ← n

n ← r return m

How do we know that Euclid’s algorithm eventually comes to a stop? This follows from the observation that the second integer of the pair gets smaller with each iteration and it cannot become negative. Indeed, the new value of n on the next iteration is m mod n, which is always smaller than n (why?). Hence, the value of the second integer eventually becomes 0, and the algorithm stops.

Just as with many other problems, there are several algorithms for computing the greatest common divisor. Let us look at the other two methods for this prob-lem. The first is simply based on the definition of the greatest common divisor of m and n as the largest integer that divides both numbers evenly. Obviously, such a common divisor cannot be greater than the smaller of these numbers, which we will denote by t = min{m, n}. So we can start by checking whether t divides both m and n: if it does, t is the answer; if it does not, we simply decrease t by 1 and try again. (How do we know that the process will eventually stop?) For example, for numbers 60 and 24, the algorithm will try first 24, then 23, and so on, until it reaches 12, where it stops.

Consecutive integer checking algorithm for computing gcd(m, n)

Step 1 Assign the value of min{m, n} to t.

Step 2 Divide m by t. If the remainder of this division is 0, go to Step 3; otherwise, go to Step 4.

Step 3 Divide n by t. If the remainder of this division is 0, return the value of t as the answer and stop; otherwise, proceed to Step 4.

Step 4 Decrease the value of t by 1. Go to Step 2.

Note that unlike Euclid’s algorithm, this algorithm, in the form presented, does not work correctly when one of its input numbers is zero. This example illustrates why it is so important to specify the set of an algorithm’s inputs explicitly and carefully.

The third procedure for finding the greatest common divisor should be famil-iar to you from middle school.

Middle-school procedure for computing gcd(m, n)

Step 1 Find the prime factors of m. Step 2 Find the prime factors of n.

Step 3 Identify all the common factors in the two prime expansions found in Step 1 and Step 2. (If p is a common factor occurring p_m and p_n times in m and n, respectively, it should be repeated min{p_m, p_n} times.)

Step 4 Compute the product of all the common factors and return it as the greatest common divisor of the numbers given.

Thus, for the numbers 60 and 24, we get

60 = 2 ^. 2 ^. 3 ^. 5

24 = 2 ^. 2 ^. 2 ^. 3 gcd(60, 24) = 2 ^. 2 ^. 3 = 12.

Nostalgia for the days when we learned this method should not prevent us from noting that the last procedure is much more complex and slower than Euclid’s algorithm. (We will discuss methods for finding and comparing running times of algorithms in the next chapter.) In addition to inferior efficiency, the middle-school procedure does not qualify, in the form presented, as a legitimate algorithm. Why? Because the prime factorization steps are not defined unambiguously: they require a list of prime numbers, and I strongly suspect that your middle-school math teacher did not explain how to obtain such a list. This is not a matter of unnecessary nitpicking. Unless this issue is resolved, we cannot, say, write a program implementing this procedure. Incidentally, Step 3 is also not defined clearly enough. Its ambiguity is much easier to rectify than that of the factorization steps, however. How would you find common elements in two sorted lists?

So, let us introduce a simple algorithm for generating consecutive primes not exceeding any given integer n > 1. It was probably invented in ancient Greece and is known as the sieve of Eratosthenes (ca. 200 B.C.). The algorithm starts by initializing a list of prime candidates with consecutive integers from 2 to n. Then, on its first iteration, the algorithm eliminates from the list all multiples of 2, i.e., 4, 6, and so on. Then it moves to the next item on the list, which is 3, and eliminates its multiples. (In this straightforward version, there is an overhead because some numbers, such as 6, are eliminated more than once.) No pass for number 4 is needed: since 4 itself and all its multiples are also multiples of 2, they were already eliminated on a previous pass. The next remaining number on the list, which is used on the third pass, is 5. The algorithm continues in this fashion until no more numbers can be eliminated from the list. The remaining integers of the list are the primes needed.

As an example, consider the application of the algorithm to finding the list of primes not exceeding n = 25:

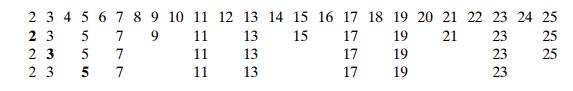
For this example, no more passes are needed because they would eliminate num-bers already eliminated on previous iterations of the algorithm. The remaining numbers on the list are the consecutive primes less than or equal to 25.

What is the largest number p whose multiples can still remain on the list to make further iterations of the algorithm necessary? Before we answer this question, let us first note that if p is a number whose multiples are being eliminated on the current pass, then the first multiple we should consider is p ^. p because all its smaller multiples 2p, . . . , (p − 1)p have been eliminated on earlier passes through the list. This observation helps to avoid eliminating the same number more than

ALGORITHM                 Sieve(n)

//Implements the sieve of Eratosthenes //Input: A positive integer n > 1

//Output: Array L of all prime numbers less than or equal to n

So now we can incorporate the sieve of Eratosthenes into the middle-school procedure to get a legitimate algorithm for computing the greatest common divi-sor of two positive integers. Note that special care needs to be exercised if one or both input numbers are equal to 1: because mathematicians do not consider 1 to be a prime number, strictly speaking, the method does not work for such inputs.

Before we leave this section, one more comment is in order. The exam-ples considered in this section notwithstanding, the majority of algorithms in use today—even those that are implemented as computer programs—do not deal with mathematical problems. Look around for algorithms helping us through our daily routines, both professional and personal. May this ubiquity of algorithms in to-day’s world strengthen your resolve to learn more about these fascinating engines of the information age.

Exercises 1.1

Do some research on al-Khorezmi (also al-Khwarizmi), the man from whose name the word “algorithm” is derived. In particular, you should learn what the origins of the words “algorithm” and “algebra” have in common.

Given that the official purpose of the U.S. patent system is the promotion of the “useful arts,” do you think algorithms are patentable in this country? Should they be?

a. Write down driving directions for going from your school to your home with the precision required from an algorithm’s description.

b. Write down a recipe for cooking your favorite dish with the precision required by an algorithm.

5. Design an algorithm to find all the common elements in two sorted lists of numbers. For example, for the lists 2, 5, 5, 5 and 2, 2, 3, 5, 5, 7, the output should be 2, 5, 5. What is the maximum number of comparisons your algorithm makes if the lengths of the two given lists are m and n, respectively?

a.  Find gcd(31415, 14142) by applying Euclid’s algorithm.

Estimate how many times faster it will be to find gcd(31415, 14142) by Euclid’s algorithm compared with the algorithm based on checking con-secutive integers from min{m, n} down to gcd(m, n).

Prove the equality gcd(m, n) = gcd(n, m mod n) for every pair of positive integers m and n.

What does Euclid’s algorithm do for a pair of integers in which the first is smaller than the second? What is the maximum number of times this can happen during the algorithm’s execution on such an input?

a. What is the minimum number of divisions made by Euclid’s algorithm among all inputs 1 ≤ m, n ≤ 10?

What is the maximum number of divisions made by Euclid’s algorithm among all inputs 1 ≤ m, n ≤ 10?

a. Euclid’s algorithm, as presented in Euclid’s treatise, uses subtractions rather than integer divisions. Write pseudocode for this version of Euclid’s algorithm.

Euclid’s game (see [Bog]) starts with two unequal positive integers on the board. Two players move in turn. On each move, a player has to write on the board a positive number equal to the difference of two numbers already on the board; this number must be new, i.e., different from all the numbers already on the board. The player who cannot move loses the game. Should you choose to move first or second in this game?

The extended Euclid’s algorithm determines not only the greatest common divisor d of two positive integers m and n but also integers (not necessarily positive) x and y, such that mx + ny = d.

Look up a description of the extended Euclid’s algorithm (see, e.g., [KnuI, p. 13]) and implement it in the language of your choice.

Modify your program to find integer solutions to the Diophantine equation ax + by = c with any set of integer coefficients a, b, and c.

Locker doors There are n lockers in a hallway, numbered sequentially from 1 to n. Initially, all the locker doors are closed. You make n passes by the lockers, each time starting with locker #1. On the ith pass, i = 1, 2, . . . , n, you toggle the door of every ith locker: if the door is closed, you open it; if it is open, you close it. After the last pass, which locker doors are open and which are closed? How many of them are open?