Example: Computing the nth Fibonacci Number

Example: Computing the nth Fibonacci Number

The Fibonacci numbers were introduced by Leonardo Fibonacci in 1202 as a solution to a problem about the size of a rabbit population (Problem 2 in this section’s exercises). Many more examples of Fibonacci-like numbers have since been discovered in the natural world, and they have even been used in predicting the prices of stocks and commodities. There are some interesting applications of the Fibonacci numbers in computer science as well. For example, worst-case inputs for Euclid’s algorithm discussed in Section 1.1 happen to be consecutive elements of the Fibonacci sequence. In this section, we briefly consider algorithms for computing the nth element of this sequence. Among other benefits, the discussion will provide us with an opportunity to introduce another method for solving recurrence relations useful for analysis of recursive algorithms.

To start, let us get an explicit formula for F (n). If we try to apply the method of backward substitutions to solve recurrence (2.6), we will fail to get an easily discernible pattern. Instead, we can take advantage of a theorem that describes solutions to a homogeneous second-order linear recurrence with constant co-efficients

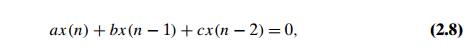
where a, b, and c are some fixed real numbers (a  = 0) called the coefficients of the recurrence and x(n) is the generic term of an unknown sequence to be found. Applying this theorem to our recurrence with the initial conditions given—see Appendix B—we obtain the formula

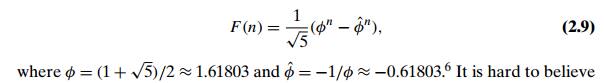
that formula (2.9), which includes arbitrary integer powers of irrational numbers, yields nothing else but all the elements of Fibonacci sequence (2.5), but it does!

One of the benefits of formula (2.9) is that it immediately implies that F (n) grows exponentially (remember Fibonacci’s rabbits?), i.e., F (n) ∈ ѳ(φⁿ). This

In the algorithms that follow, we consider, for the sake of simplicity, such oper-ations as additions and multiplications at unit cost. Since the Fibonacci numbers grow infinitely large (and grow very rapidly), a more detailed analysis than the one offered here is warranted. In fact, it is the size of the numbers rather than a time-efficient method for computing them that should be of primary concern here. Still, these caveats notwithstanding, the algorithms we outline and their analysis provide useful examples for a student of the design and analysis of algorithms.

To begin with, we can use recurrence (2.6) and initial conditions (2.7) for the obvious recursive algorithm for computing F (n).

ALGORITHM     F (n)

//Computes the nth Fibonacci number recursively by using its definition //Input: A nonnegative integer n

//Output: The nth Fibonacci number if n ≤ 1 return n

else return F (n − 1) + F (n − 2)

Before embarking on its formal analysis, can you tell whether this is an effi-cient algorithm? Well, we need to do a formal analysis anyway. The algorithm’s ba-sic operation is clearly addition, so let A(n) be the number of additions performed by the algorithm in computing F (n). Then the numbers of additions needed for computing F (n − 1) and F (n − 2) are A(n − 1) and A(n − 2), respectively, and the algorithm needs one more addition to compute their sum. Thus, we get the following recurrence for A(n):

The recurrence A(n) − A(n − 1) − A(n − 2) = 1 is quite similar to recurrence F (n) − F (n − 1) − F (n − 2) = 0, but its right-hand side is not equal to zero. Such recurrences are called inhomogeneous. There are general techniques for solving inhomogeneous recurrences (see Appendix B or any textbook on discrete mathe-matics), but for this particular recurrence, a special trick leads to a faster solution. We can reduce our inhomogeneous recurrence to a homogeneous one by rewriting it as

[A(n) + 1] − [A(n − 1) + 1] − [A(n − 2) + 1] = 0

and substituting B(n) = A(n) + 1

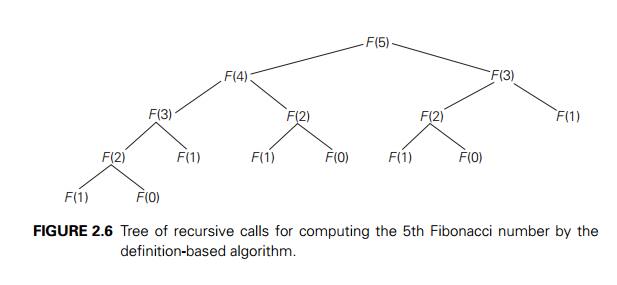
          The poor efficiency class of the algorithm could be anticipated by the nature of recurrence (2.11). Indeed, it contains two recursive calls with the sizes of smaller instances only slightly smaller than size n. (Have you encountered such a situation before?) We can also see the reason behind the algorithm’s inefficiency by looking at a recursive tree of calls tracing the algorithm’s execution. An example of such a tree for n = 5 is given in Figure 2.6. Note that the same values of the function are being evaluated here again and again, which is clearly extremely inefficient.

          We can obtain a much faster algorithm by simply computing the successive elements of the Fibonacci sequence iteratively, as is done in the following algorithm.

ALGORITHM      Fib(n)

          //Computes the nth Fibonacci number iteratively by using its definition

          //Input: A nonnegative integer n

          //Output: The nth Fibonacci number

          F [0] ← 0; F [1] ← 1

          for i ← 2 to n do

          F [i] ← F [i − 1] + F [i − 2]

          return F [n]

This algorithm clearly makes n − 1 additions. Hence, it is linear as a function of n and “only” exponential as a function of the number of bits b in n’s binary representation. Note that using an extra array for storing all the preceding ele-ments of the Fibonacci sequence can be avoided: storing just two values is neces-sary to accomplish the task (see Problem 8 in this section’s exercises).

The third alternative for computing the nth Fibonacci number lies in using formula (2.10). The efficiency of the algorithm will obviously be determined by the efficiency of an exponentiation algorithm used for computing φⁿ. If it is done by simply multiplying φ by itself n − 1 times, the algorithm will be in (n) = (2^b). There are faster algorithms for the exponentiation problem. For example, we will discuss (log n) = (b) algorithms for this problem in Chapters 4 and 6. Note also that special care should be exercised in implementing this approach to computing the nth Fibonacci number. Since all its intermediate results are irrational numbers, we would have to make sure that their approximations in the computer are accurate enough so that the final round-off yields a correct result.

Finally, there exists a (log n) algorithm for computing the nth Fibonacci number that manipulates only integers. It is based on the equality

and an efficient way of computing matrix powers.

Exercises 2.5

            1. Find a Web site dedicated to applications of the Fibonacci numbers and study it.

            2. Fibonacci’s rabbits problem A man put a pair of rabbits in a place sur-rounded by a wall. How many pairs of rabbits will be there in a year if the initial pair of rabbits (male and female) are newborn and all rabbit pairs are not fertile during their first month of life but thereafter give birth to one new male/female pair at the end of every month?

            3. Climbing stairs Find the number of different ways to climb an n-stair stair-case if each step is either one or two stairs. For example, a 3-stair staircase can be climbed three ways: 1-1-1, 1-2, and 2-1.

4. How many even numbers are there among the first n Fibonacci numbers, i.e., among the numbers F (0), F (1), . . . , F (n − 1)? Give a closed-form formula valid for every n > 0.

            6. The maximum values of the Java primitive types int and long are 2³¹ − 1 and 2⁶³ − 1, respectively. Find the smallest n for which the nth Fibonacci number is not going to fit in a memory allocated for 

a. the type int.

b. the type long.

            7. Consider the recursive definition-based algorithm for computing the nth Fi-

bonacci number F (n). Let C(n) and Z(n) be the number of times F (1) and F (0) are computed, respectively. Prove that

            C(n) = F (n).b. Z(n) = F (n − 1).

            8. Improve algorithm F ib of the text so that it requires only  (1) space.

9. Prove the equality

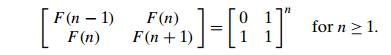
            10. How many modulo divisions are made by Euclid’s algorithm on two consec-utive Fibonacci numbers F (n) and F (n − 1) as the algorithm’s input?

            11. Dissecting a Fibonacci rectangle Given a rectangle whose sides are two con-secutive Fibonacci numbers, design an algorithm to dissect it into squares with no more than two squares being the same size. What is the time efficiency class of your algorithm?

           12. In the language of your choice, implement two algorithms for computing the last five digits of the nth Fibonacci number that are based on (a) the recursive definition-based algorithm F (n); (b) the iterative definition-based algorithm Fib(n). Perform an experiment to find the largest value of n for which your programs run under 1 minute on your computer.