Asymptotic Notations and Basic Efficiency Classes

Asymptotic Notations and Basic Efficiency Classes

1. Informal Introduction

2. O-notation

3. Omagha -notation

4. 0-notation

5. Useful Property Involving the Asymptotic Notations

6. Using Limits for Comparing Orders of Growth

7. Basic Efficiency Classes

8. Exercises

As pointed out in the previous section, the efficiency analysis framework con-centrates on the order of growth of an algorithm’s basic operation count as the principal indicator of the algorithm’s efficiency. To compare and rank such orders of growth, computer scientists use three notations: O (big oh), (big omega), and (big theta). First, we introduce these notations informally, and then, after sev-eral examples, formal definitions are given. In the following discussion, t (n) and g(n) can be any nonnegative functions defined on the set of natural numbers. In the context we are interested in, t (n) will be an algorithm’s running time (usually indicated by its basic operation count C(n)), and g(n) will be some simple function to compare the count with.

Informal Introduction

Informally, O(g(n)) is the set of all functions with a lower or same order of growth as g(n) (to within a constant multiple, as n goes to infinity). Thus, to give a few examples, the following assertions are all true:

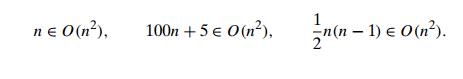
Indeed, the first two functions are linear and hence have a lower order of growth than g(n) = n², while the last one is quadratic and hence has the same order of growth as n². On the other hand,

Indeed, the functions n³ and 0.00001n³ are both cubic and hence have a higher order of growth than n², and so has the fourth-degree polynomial n⁴ + n + 1.

The second notation,  (g(n)), stands for the set of all functions with a higher or same order of growth as g(n) (to within a constant multiple, as n goes to infinity). For example,

Finally,  (g(n)) is the set of all functions that have the same order of growth as g(n) (to within a constant multiple, as n goes to infinity). Thus, every quadratic function an² + bn + c with a > 0 is in  (n²), but so are, among infinitely many others, n² + sin n and n² + log n. (Can you explain why?)

Hopefully, this informal introduction has made you comfortable with the idea behind the three asymptotic notations. So now come the formal definitions.

O-notation

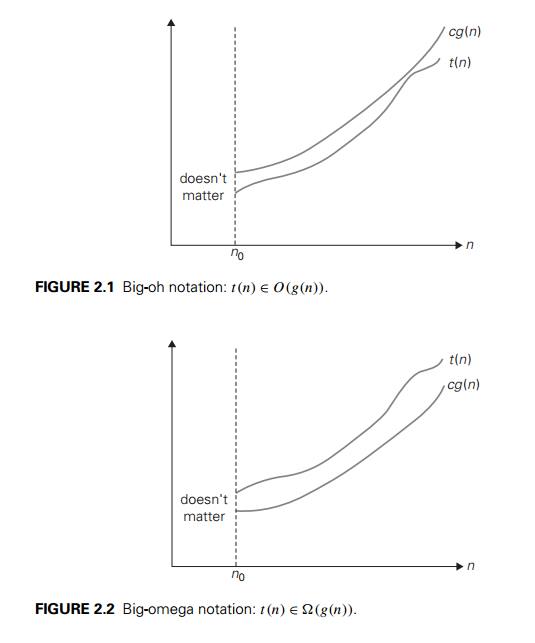
DEFINITION A function t (n) is said to be in O(g(n)), denoted t (n) ∈ O(g(n)), if t (n) is bounded above by some constant multiple of g(n) for all large n, i.e., if there exist some positive constant c and some nonnegative integer n₀ such that

t (n) ≤ cg(n)                          for all n ≥ n₀.

The definition is illustrated in Figure 2.1 where, for the sake of visual clarity, n is extended to be a real number.

As an example, let us formally prove one of the assertions made in the introduction: 100n + 5 ∈ O(n²). Indeed,

100n + 5 ≤ 100n + n (for all n ≥ 5) = 101n ≤ 101n².

Thus, as values of the constants c and n₀ required by the definition, we can take 101 and 5, respectively.

Note that the definition gives us a lot of freedom in choosing specific values for constants c and n₀. For example, we could also reason that

100n + 5 ≤ 100n + 5n (for all n ≥ 1) = 105n

to complete the proof with c = 105 and n₀ = 1.

Ω-notation

DEFINITION A function t (n) is said to be in  (g(n)), denoted t (n) ∈  (g(n)), if t (n) is bounded below by some positive constant multiple of g(n) for all large n, i.e., if there exist some positive constant c and some nonnegative integer n₀ such that

t (n) ≥ cg(n)                          for all n ≥ n₀.

The definition is illustrated in Figure 2.2.

Here is an example of the formal proof that n³ ∈  (n²):

n³ ≥ n²                                 for all n ≥ 0,

i.e., we can select c = 1 and n₀ = 0.

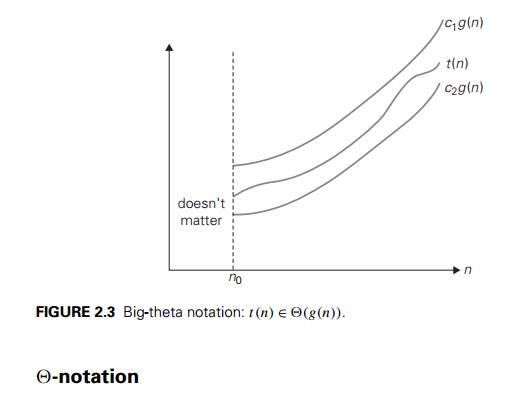
DEFINITION A function t (n) is said to be in  (g(n)), denoted t (n) ∈  (g(n)), if t (n) is bounded both above and below by some positive constant multiples of g(n) for all large n, i.e., if there exist some positive constants c₁ and c₂ and some nonnegative integer n₀ such that

c₂g(n) ≤ t (n) ≤ c₁g(n)               for all n ≥ n₀.

The definition is illustrated in Figure 2.3.

For example, let us prove that ₂¹ n(n − 1) ∈  (n²). First, we prove the right inequality (the upper bound):

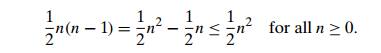
Second, we prove the left inequality (the lower bound):

Useful Property Involving the Asymptotic Notations

Using the formal definitions of the asymptotic notations, we can prove their general properties (see Problem 7 in this section’s exercises for a few simple examples). The following property, in particular, is useful in analyzing algorithms that comprise two consecutively executed parts.

THEOREM                  If t₁(n) ∈ O(g₁(n)) and t₂(n) ∈ O(g₂(n)), then

t₁(n) + t₂(n) ∈ O(max{g₁(n), g₂(n)}).

(The analogous assertions are true for the        and  notations as well.)

PROOF                    The proof extends to orders of growth the following simple fact about

four arbitrary real numbers a₁, b₁, a₂, b₂: if a₁ ≤ b₁ and a₂ ≤ b₂, then a₁ + a₂ ≤ 2 max{b₁, b₂}.

Since t₁(n) ∈ O(g₁(n)), there exist some positive constant c₁ and some non-negative integer n₁ such that

t₁(n) ≤ c₁g₁(n)                                              for all n ≥ n₁.

Similarly, since t₂(n) ∈ O(g₂(n)),

t₂(n) ≤ c₂g₂(n)                                               for all n ≥ n₂.

Let us denote c₃ = max{c₁, c₂} and consider n ≥ max{n₁, n₂} so that we can use both inequalities. Adding them yields the following:

t₁(n) + t₂(n) ≤ c₁g₁(n) + c₂g₂(n)

c₃g₁(n) + c₃g₂(n) = c₃[g₁(n) + g₂(n)]

c₃2 max{g₁(n), g₂(n)}.

Hence, t₁(n) + t₂(n) ∈ O(max{g₁(n), g₂(n)}), with the constants c and n₀ required by the O definition being 2c₃ = 2 max{c₁, c₂} and max{n₁, n₂}, respectively.

So what does this property imply for an algorithm that comprises two consec-utively executed parts? It implies that the algorithm’s overall efficiency is deter-mined by the part with a higher order of growth, i.e., its least efficient part:

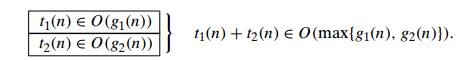
For example, we can check whether an array has equal elements by the following two-part algorithm: first, sort the array by applying some known sorting algorithm; second, scan the sorted array to check its consecutive elements for equality. If, for example, a sorting algorithm used in the first part makes no more than ₂¹ n(n − 1) comparisons (and hence is in O(n²)) while the second part makes no more than n − 1 comparisons (and hence is in O(n)), the efficiency of the entire algorithm will be in O(max{n², n}) = O(n²).

Using Limits for Comparing Orders of Growth

Though the formal definitions of O, ѳ, and Ω are indispensable for proving their abstract properties, they are rarely used for comparing the orders of growth of two specific functions. A much more convenient method for doing so is based on computing the limit of the ratio of two functions in question. Three principal cases may arise:

Here are three examples of using the limit-based approach to comparing orders of growth of two functions.

EXAMPLE 1 Compare the orders of growth of ₂¹ n(n − 1) and n². (This is one of the examples we used at the beginning of this section to illustrate the definitions.)

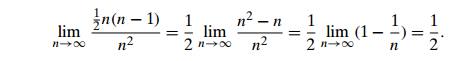
Since the limit is equal to a positive constant, the functions have the same order of growth or, symbolically, ₂¹ n(n − 1) ∈ ѳ(n²).

Thus, though 2ⁿ grows very fast, n! grows still faster. We can write symbolically that n! ∈ Ω (2ⁿ); note, however, that while the big-Omega notation does not preclude the possibility that n! and 2ⁿ have the same order of growth, the limit computed here certainly does.

Basic Efficiency Classes

Even though the efficiency analysis framework puts together all the functions whose orders of growth differ by a constant multiple, there are still infinitely many such classes. (For example, the exponential functions aⁿ have different orders of growth for different values of base a.) Therefore, it may come as a surprise that the time efficiencies of a large number of algorithms fall into only a few classes. These classes are listed in Table 2.2 in increasing order of their orders of growth, along with their names and a few comments.

You could raise a concern that classifying algorithms by their asymptotic effi-ciency would be of little practical use since the values of multiplicative constants are usually left unspecified. This leaves open the possibility of an algorithm in a worse efficiency class running faster than an algorithm in a better efficiency class for inputs of realistic sizes. For example, if the running time of one algorithm is n3 while the running time of the other is 106n2, the cubic algorithm will outperform the quadratic algorithm unless n exceeds 106. A few such anomalies are indeed known. Fortunately, multiplicative constants usually do not differ that drastically. As a rule, you should expect an algorithm from a better asymptotic efficiency class to outperform an algorithm from a worse class even for moderately sized inputs. This observation is especially true for an algorithm with a better than exponential running time versus an exponential (or worse) algorithm.

Exercises 2.2

Use the most appropriate notation among O, Ω, and ѳ and to indicate the time efficiency class of sequential search (see Section 2.1)

in the worst case.

in the best case.

in the average case.

Use the informal definitions of O, Ω, and ѳ to determine whether the follow-ing assertions are true or false.

4 a. Table 2.1 contains values of several functions that often arise in the analysis of algorithms. These values certainly suggest that the functions

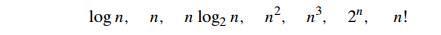
are listed in increasing order of their order of growth. Do these values prove this fact with mathematical certainty?

Prove that the functions are indeed listed in increasing order of their order of growth.

5 List the following functions according to their order of growth from the lowest to the highest:

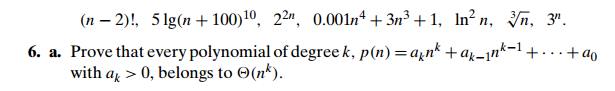
b.Prove that exponential functions a-power(n) have different orders of growth for different values of base a > 0.

7 Prove the following assertions by using the definitions of the notations in-volved, or disprove them by giving a specific counterexample.

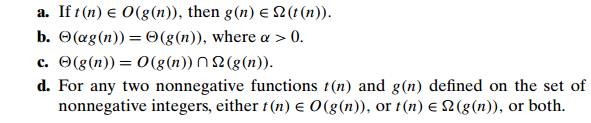
 8 Prove the section’s theorem for

a.       ѳ  notation. b.    Ωnotation.

                                                              9      We mentioned in this section that one can check whether all elements of an array are distinct by a two-part algorithm based on the array’s presorting.

                                                                            If the presorting is done by an algorithm with a time efficiency in (n log n), what will be a time-efficiency class of the entire algorithm?

                                                                            If the sorting algorithm used for presorting needs an extra array of size n, what will be the space-efficiency class of the entire algorithm?

                        10  The range of a finite nonempty set of n real numbers S is defined as the differ-ence between the largest and smallest elements of S. For each representation of S given below, describe in English an algorithm to compute the range. Indi-cate the time efficiency classes of these algorithms using the most appropriate notation (O, Ω, or ѳ).

                                                                            An unsorted array

                                                                            A sorted array

                                                                            A sorted singly linked list

                                                                            A binary search tree

                                 11   Lighter or heavier? You have n > 2 identical-looking coins and a two-pan balance scale with no weights. One of the coins is a fake, but you do not know whether it is lighter or heavier than the genuine coins, which all weigh the same. Design a  (1) algorithm to determine whether the fake coin is lighter or heavier than the others.

                                     12 Door in a wall You are facing a wall that stretches infinitely in both direc-tions. There is a door in the wall, but you know neither how far away nor in which direction. You can see the door only when you are right next to it. De-sign an algorithm that enables you to reach the door by walking at most O(n) steps where n is the (unknown to you) number of steps between your initial position and the door. [Par95]