Selection Sort and Bubble Sort

Selection Sort and Bubble Sort

In this section, we consider the application of the brute-force approach to the problem of sorting: given a list of n orderable items (e.g., numbers, characters from some alphabet, character strings), rearrange them in nondecreasing order. As we mentioned in Section 1.3, dozens of algorithms have been developed for solving this very important problem. You might have learned several of them in the past. If you have, try to forget them for the time being and look at the problem afresh.

Now, after your mind is unburdened of previous knowledge of sorting algorithms, ask yourself a question: “What would be the most straightforward method for solving the sorting problem?” Reasonable people may disagree on the answer to this question. The two algorithms discussed here—selection sort and bubble sort—seem to be the two prime candidates.

Selection Sort

We start selection sort by scanning the entire given list to find its smallest element and exchange it with the first element, putting the smallest element in its final position in the sorted list. Then we scan the list, starting with the second element, to find the smallest among the last n − 1 elements and exchange it with the second element, putting the second smallest element in its final position. Generally, on the ith pass through the list, which we number from 0 to n − 2, the algorithm searches for the smallest item among the last n − i elements and swaps it with A_i:

After n − 1 passes, the list is sorted.

Here is pseudocode of this algorithm, which, for simplicity, assumes that the list is implemented as an array:

ALGORITHM     SelectionSort(A[0..n − 1])

//Sorts a given array by selection sort

//Input: An array A[0..n − 1] of orderable elements //Output: Array A[0..n − 1] sorted in nondecreasing order for i ← 0 to n − 2 do

min ← i

for j ← i + 1 to n − 1 do

if A[j ] < A[min] min ← j swap A[i] and A[min]

As an example, the action of the algorithm on the list 89, 45, 68, 90, 29, 34, 17 is illustrated in Figure 3.1.

The analysis of selection sort is straightforward. The input size is given by the number of elements n; the basic operation is the key comparison A[j ] < A[min]. The number of times it is executed depends only on the array size and is given by the following sum:

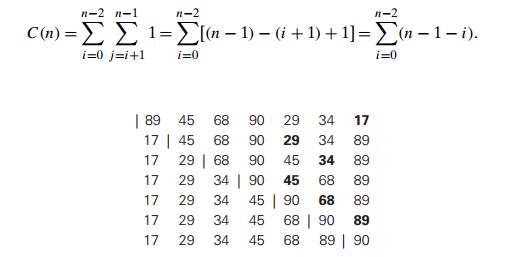
FIGURE 3.1 Example of sorting with selection sort. Each line corresponds to one iteration of the algorithm, i.e., a pass through the list’s tail to the right of the vertical bar; an element in bold indicates the smallest element found. Elements to the left of the vertical bar are in their final positions and are not considered in this and subsequent iterations.

Since we have already encountered the last sum in analyzing the algorithm of Example 2 in Section 2.3, you should be able to compute it now on your own. Whether you compute this sum by distributing the summation symbol or by immediately getting the sum of decreasing integers, the answer, of course, must be the same:

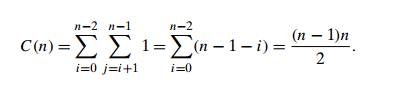
Thus, selection sort is a  (n²) algorithm on all inputs. Note, however, that the number of key swaps is only  (n), or, more precisely, n − 1 (one for each repetition of the i loop). This property distinguishes selection sort positively from many other sorting algorithms.

Bubble Sort

Another brute-force application to the sorting problem is to compare adjacent elements of the list and exchange them if they are out of order. By doing it repeatedly, we end up “bubbling up” the largest element to the last position on the list. The next pass bubbles up the second largest element, and so on, until after n − 1 passes the list is sorted. Pass i (0 ≤ i ≤ n − 2) of bubble sort can be represented by the following diagram:

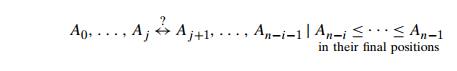
Here is pseudocode of this algorithm.

ALGORITHM                 BubbleSort(A[0..n − 1])

//Sorts a given array by bubble sort

//Input: An array A[0..n − 1] of orderable elements //Output: Array A[0..n − 1] sorted in nondecreasing order for i ← 0 to n − 2 do

for j ← 0 to n − 2 − i do

if A[j + 1] < A[j ] swap A[j ] and A[j + 1]

The action of the algorithm on the list 89, 45, 68, 90, 29, 34, 17 is illustrated as an example in Figure 3.2.

The number of key comparisons for the bubble-sort version given above is the same for all arrays of size n; it is obtained by a sum that is almost identical to the sum for selection sort:

FIGURE 3.2 First two passes of bubble sort on the list 89, 45, 68, 90, 29, 34, 17. A new line is shown after a swap of two elements is done. The elements to the right of the vertical bar are in their final positions and are not considered in subsequent iterations of the algorithm.

The number of key swaps, however, depends on the input. In the worst case of decreasing arrays, it is the same as the number of key comparisons:

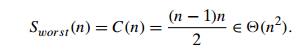
As is often the case with an application of the brute-force strategy, the first version of an algorithm obtained can often be improved upon with a modest amount of effort. Specifically, we can improve the crude version of bubble sort given above by exploiting the following observation: if a pass through the list makes no exchanges, the list has been sorted and we can stop the algorithm (Problem 12a in this section’s exercises). Though the new version runs faster on some inputs, it is still in  (n²) in the worst and average cases. In fact, even among elementary sorting methods, bubble sort is an inferior choice, and if it were not for its catchy name, you would probably have never heard of it. However, the general lesson you just learned is important and worth repeating:

A first application of the brute-force approach often results in an algorithm that can be improved with a modest amount of effort.

Exercises 3.1

1. a. Give an example of an algorithm that should not be considered an appli-cation of the brute-force approach.

            b. Give an example of a problem that cannot be solved by a brute-force algorithm.

           2. a. What is the time efficiency of the brute-force algorithm for computing aⁿ as a function of n? As a function of the number of bits in the binary representation of n?

            b. If you are to compute aⁿ mod m where a > 1 and n is a large positive integer, how would you circumvent the problem of a very large magnitude of aⁿ?

            3. For each of the algorithms in Problems 4, 5, and 6 of Exercises 2.3, tell whether or not the algorithm is based on the brute-force approach.

            a.  Design a brute-force algorithm for computing the value of a polynomial

at a given point x₀ and determine its worst-case efficiency class.

          b.   If the algorithm you designed is in  (n²), design a linear algorithm for this problem.

            c. Is it possible to design an algorithm with a better-than-linear efficiency for this problem?

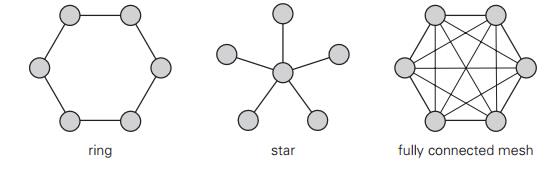
5. A network topology specifies how computers, printers, and other devices are connected over a network. The figure below illustrates three common topologies of networks: the ring, the star, and the fully connected mesh.

You are given a boolean matrix A[0..n − 1, 0..n − 1], where n > 3, which is supposed to be the adjacency matrix of a graph modeling a network with one of these topologies. Your task is to determine which of these three topologies, if any, the matrix represents. Design a brute-force algorithm for this task and indicate its time efficiency class.

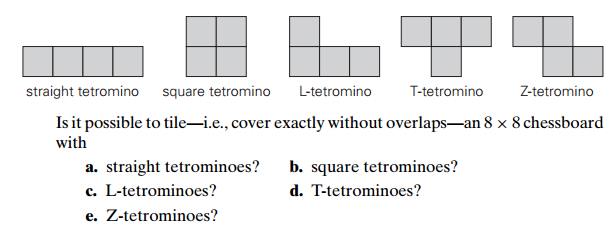
6. Tetromino tilings Tetrominoes are tiles made of four 1 × 1 squares. There are five types of tetrominoes shown below:

            7. A stack of fake coins There are n stacks of n identical-looking coins. All of the coins in one of these stacks are counterfeit, while all the coins in the other stacks are genuine. Every genuine coin weighs 10 grams; every fake weighs 11 grams. You have an analytical scale that can determine the exact weight of any number of coins.

            Devise a brute-force algorithm to identify the stack with the fake coins and determine its worst-case efficiency class.

            What is the minimum number of weighings needed to identify the stack with the fake coins?

            8. Sort the list E, X, A, M, P , L, E in alphabetical order by selection sort.

            9. Is selection sort stable? (The definition of a stable sorting algorithm was given in Section 1.3.)

            10. Is it possible to implement selection sort for linked lists with the same  (n²) efficiency as the array version?

            11. Sort the list E, X, A, M, P , L, E in alphabetical order by bubble sort.

            12. a. Prove that if bubble sort makes no exchanges on its pass through a list, the list is sorted and the algorithm can be stopped.

            b. Write pseudocode of the method that incorporates this improvement.

            c. Prove that the worst-case efficiency of the improved version is quadratic.

           13. Is bubble sort stable?

            14 . Alternating disks You have a row of 2n disks of two colors, n dark and n light. They alternate: dark, light, dark, light, and so on. You want to get all the dark disks to the right-hand end, and all the light disks to the left-hand end. The only moves you are allowed to make are those that interchange the positions of two neighboring disks.

Design an algorithm for solving this puzzle and determine the number of moves it takes. [Gar99] Brute Force and Exhaustive Search