Closest-Pair and Convex-Hull Problems by Brute Force

Closest-Pair and Convex-Hull Problems by Brute Force

In this section, we consider a straightforward approach to two well-known prob-lems dealing with a finite set of points in the plane. These problems, aside from their theoretical interest, arise in two important applied areas: computational ge-ometry and operations research.

Closest-Pair Problem

The closest-pair problem calls for finding the two closest points in a set of n points. It is the simplest of a variety of problems in computational geometry that deals with proximity of points in the plane or higher-dimensional spaces. Points in question can represent such physical objects as airplanes or post offices as well as database records, statistical samples, DNA sequences, and so on. An air-traffic controller might be interested in two closest planes as the most probable collision candidates. A regional postal service manager might need a solution to the closest-pair problem to find candidate post-office locations to be closed.

One of the important applications of the closest-pair problem is cluster analy-sis in statistics. Based on n data points, hierarchical cluster analysis seeks to orga-nize them in a hierarchy of clusters based on some similarity metric. For numerical data, this metric is usually the Euclidean distance; for text and other nonnumerical data, metrics such as the Hamming distance (see Problem 5 in this section’s ex-ercises) are used. A bottom-up algorithm begins with each element as a separate cluster and merges them into successively larger clusters by combining the closest pair of clusters.

For simplicity, we consider the two-dimensional case of the closest-pair prob-lem. We assume that the points in question are specified in a standard fashion by their (x, y) Cartesian coordinates and that the distance between two points p_i(x_i, y_i) and p_j (x_j , y_j ) is the standard Euclidean distance

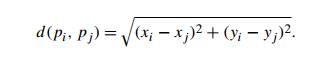
The brute-force approach to solving this problem leads to the following ob-vious algorithm: compute the distance between each pair of distinct points and find a pair with the smallest distance. Of course, we do not want to compute the distance between the same pair of points twice. To avoid doing so, we consider only the pairs of points (p_i, p_j ) for which i < j .

  Closest-Pair and Convex-Hull Problems by Brute Force

Pseudocode below computes the distance between the two closest points; getting the closest points themselves requires just a trivial modification.

ALGORITHM     BruteForceClosestPair(P )

//Finds distance between two closest points in the plane by brute force

//Input: A list P of n (n ≥ 2) points p₁(x₁, y₁), . . . , p_n(x_n, y_n) //Output: The distance between the closest pair of points

d ← ∞

for i ← 1 to n − 1 do

for j ← i + 1 to n do

d ← min(d, sqrt((x_i − x_j )² + (y_i − y_j )²)) //sqrt is square root

return d

The basic operation of the algorithm is computing the square root. In the age of electronic calculators with a square-root button, one might be led to believe that computing the square root is as simple an operation as, say, addition or multiplication. Of course, it is not. For starters, even for most integers, square roots are irrational numbers that therefore can be found only approximately. Moreover, computing such approximations is not a trivial matter. But, in fact, computing square roots in the loop can be avoided! (Can you think how?) The trick is to realize that we can simply ignore the square-root function and compare the values (x_i − x_j )² + (y_i − y_j )² themselves. We can do this because the smaller a number of which we take the square root, the smaller its square root, or, as mathematicians say, the square-root function is strictly increasing.

Then the basic operation of the algorithm will be squaring a number. The number of times it will be executed can be computed as follows:

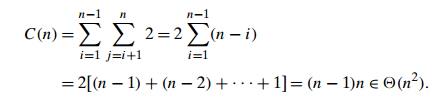
Of course, speeding up the innermost loop of the algorithm could only de-crease the algorithm’s running time by a constant factor (see Problem 1 in this section’s exercises), but it cannot improve its asymptotic efficiency class. In Chap-ter 5, we discuss a linearithmic algorithm for this problem, which is based on a more sophisticated design technique.

Convex-Hull Problem

On to the other problem—that of computing the convex hull. Finding the convex hull for a given set of points in the plane or a higher dimensional space is one of the most important—some people believe the most important—problems in com-putational geometry. This prominence is due to a variety of applications in which this problem needs to be solved, either by itself or as a part of a larger task. Sev-eral such applications are based on the fact that convex hulls provide convenient approximations of object shapes and data sets given. For example, in computer an-imation, replacing objects by their convex hulls speeds up collision detection; the same idea is used in path planning for Mars mission rovers. Convex hulls are used in computing accessibility maps produced from satellite images by Geographic Information Systems. They are also used for detecting outliers by some statisti-cal techniques. An efficient algorithm for computing a diameter of a set of points, which is the largest distance between two of the points, needs the set’s convex hull to find the largest distance between two of its extreme points (see below). Finally, convex hulls are important for solving many optimization problems, because their extreme points provide a limited set of solution candidates.

We start with a definition of a convex set.

DEFINITION A set of points (finite or infinite) in the plane is called convex if for any two points p and q in the set, the entire line segment with the endpoints at p and q belongs to the set.

All the sets depicted in Figure 3.4a are convex, and so are a straight line, a triangle, a rectangle, and, more generally, any convex polygon,¹ a circle, and the entire plane. On the other hand, the sets depicted in Figure 3.4b, any finite set of two or more distinct points, the boundary of any convex polygon, and a circumference are examples of sets that are not convex.

Now we are ready for the notion of the convex hull. Intuitively, the convex hull of a set of n points in the plane is the smallest convex polygon that contains all of them either inside or on its boundary. If this formulation does not fire up your enthusiasm, consider the problem as one of barricading n sleeping tigers by a fence of the shortest length. This interpretation is due to D. Harel [Har92]; it is somewhat lively, however, because the fenceposts have to be erected right at the spots where some of the tigers sleep! There is another, much tamer interpretation of this notion. Imagine that the points in question are represented by nails driven into a large sheet of plywood representing the plane. Take a rubber band and stretch it to include all the nails, then let it snap into place. The convex hull is the area bounded by the snapped rubber band (Figure 3.5).

A formal definition of the convex hull that is applicable to arbitrary sets, including sets of points that happen to lie on the same line, follows.

DEFINITION The convex hull of a set S of points is the smallest convex set containing S. (The “smallest” requirement means that the convex hull of S must be a subset of any convex set containing S.)

If S is convex, its convex hull is obviously S itself. If S is a set of two points, its convex hull is the line segment connecting these points. If S is a set of three

points not on the same line, its convex hull is the triangle with the vertices at the three points given; if the three points do lie on the same line, the convex hull is the line segment with its endpoints at the two points that are farthest apart. For an example of the convex hull for a larger set, see Figure 3.6.

A study of the examples makes the following theorem an expected result.

THEOREM The convex hull of any set S of n > 2 points not all on the same line is a convex polygon with the vertices at some of the points of S. (If all the points do lie on the same line, the polygon degenerates to a line segment but still with the endpoints at two points of S.)

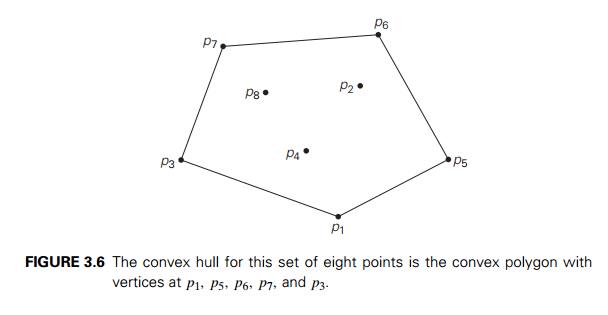
The convex-hull problem is the problem of constructing the convex hull for a given set S of n points. To solve it, we need to find the points that will serve as the vertices of the polygon in question. Mathematicians call the vertices of such a polygon “extreme points.” By definition, an extreme point of a convex set is a point of this set that is not a middle point of any line segment with endpoints in the set. For example, the extreme points of a triangle are its three vertices, the extreme points of a circle are all the points of its circumference, and the extreme points of the convex hull of the set of eight points in Figure 3.6 are p₁, p₅, p₆, p₇,

and p₃.

Extreme points have several special properties other points of a convex set do not have. One of them is exploited by the simplex method, a very important algorithm discussed in Section 10.1. This algorithm solves linear programming problems, which are problems of finding a minimum or a maximum of a linear function of n variables subject to linear constraints (see Problem 12 in this section’s exercises for an example and Sections 6.6 and 10.1 for a general discussion). Here, however, we are interested in extreme points because their identification solves the convex-hull problem. Actually, to solve this problem completely, we need to know a bit more than just which of n points of a given set are extreme points of the set’s convex hull: we need to know which pairs of points need to be connected to form the boundary of the convex hull. Note that this issue can also be addressed by listing the extreme points in a clockwise or a counterclockwise order.

So how can we solve the convex-hull problem in a brute-force manner? If you do not see an immediate plan for a frontal attack, do not be dismayed: the convex-hull problem is one with no obvious algorithmic solution. Nevertheless, there is a simple but inefficient algorithm that is based on the following observation about line segments making up the boundary of a convex hull: a line segment connecting two points p_i and p_j of a set of n points is a part of the convex hull’s boundary if and only if all the other points of the set lie on the same side of the straight line through these two points.² (Verify this property for the set in Figure 3.6.) Repeating this test for every pair of points yields a list of line segments that make up the convex hull’s boundary.

A few elementary facts from analytical geometry are needed to implement this algorithm. First, the straight line through two points (x₁, y₁), (x₂, y₂) in the coordinate plane can be defined by the equation

ax + by = c,

where a = y₂ − y₁, b = x₁ − x₂, c = x₁y₂ − y₁x₂.

Second, such a line divides the plane into two half-planes: for all the points in one of them, ax + by > c, while for all the points in the other, ax + by < c. (For the points on the line itself, of course, ax + by = c.) Thus, to check whether certain points lie on the same side of the line, we can simply check whether the expression ax + by − c has the same sign for each of these points. We leave the implementation details as an exercise.

What is the time efficiency of this algorithm? It is in O(n³): for each of n(n − 1)/2 pairs of distinct points, we may need to find the sign of ax + by − c for each of the other n − 2 points. There are much more efficient algorithms for this important problem, and we discuss one of them later in the book.

Exercises 3.3

            1. Assuming that sqrt takes about 10 times longer than each of the other oper-ations in the innermost loop of BruteForceClosestPoints, which are assumed to take the same amount of time, estimate how much faster the algorithm will run after the improvement discussed in Section 3.3.

            2. Can you design a more efficient algorithm than the one based on the brute-force strategy to solve the closest-pair problem for n points x₁, x₂, . . . , x_n on the real line?

           3. Let x₁ < x₂ < ^{. . .} < x_n be real numbers representing coordinates of n villages located along a straight road. A post office needs to be built in one of these villages.

                                 Design an efficient algorithm to find the post-office location minimizing the average distance between the villages and the post office.

                                 Design an efficient algorithm to find the post-office location minimizing the maximum distance from a village to the post office.

            4. a. There are several alternative ways to define a distance between two points p₁(x₁, y₁) and p₂(x₂, y₂) in the Cartesian plane. In particular, the Manhat-tan distance is defined as

d_M (p₁, p₂) = |x₁ − x₂| + |y₁ − y₂|.

Prove that d_M satisfies the following axioms, which every distance function must satisfy:

                                                                                        d_M (p₁, p₂) ≥ 0 for any two points p₁ and p₂, and d_M (p₁, p₂) = 0 if and only if p₁ = p₂

                                                                                        d_M (p₁, p₂) = d_M (p₂, p₁)

                                                                                        d_M (p₁, p₂) ≤ d_M (p₁, p₃) + d_M (p₃, p₂) for any p₁, p₂, and p₃

            Sketch all the points in the Cartesian plane whose Manhattan distance to the origin (0, 0) is equal to 1. Do the same for the Euclidean distance.

            True or false: A solution to the closest-pair problem does not depend on which of the two metrics—d_E (Euclidean) or d_M (Manhattan)—is used?

            5. The Hamming distance between two strings of equal length is defined as the number of positions at which the corresponding symbols are different. It is named after Richard Hamming (1915–1998), a prominent American scientist and engineer, who introduced it in his seminal paper on error-detecting and error-correcting codes.

            Does the Hamming distance satisfy the three axioms of a distance metric listed in Problem 4?

            What is the time efficiency class of the brute-force algorithm for the closest-pair problem if the points in question are strings of m symbols long and the distance between two of them is measured by the Hamming distance?

            6. Odd pie fight There are n ≥ 3 people positioned on a field (Euclidean plane) so that each has a unique nearest neighbor. Each person has a cream pie. At a signal, everybody hurls his or her pie at the nearest neighbor. Assuming that n is odd and that nobody can miss his or her target, true or false: There always remains at least one person not hit by a pie. [Car79]

7. The closest-pair problem can be posed in the k-dimensional space, in which the Euclidean distance between two points p (x₁, . . . , x_k) and p (x₁ , . . . , x_k ) is defined as

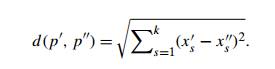
What is the time-efficiency class of the brute-force algorithm for the k-dimensional closest-pair problem?

8.   Find the convex hulls of the following sets and identify their extreme points (if they have any):

a.  a line segment

            a square

            the boundary of a square

            a straight line

9.   Design a linear-time algorithm to determine two extreme points of the convex hull of a given set of n > 1 points in the plane.

10.   What modification needs to be made in the brute-force algorithm for the convex-hull problem to handle more than two points on the same straight line?

11.   Write a program implementing the brute-force algorithm for the convex-hull problem.

12.   Consider the following small instance of the linear programming problem:

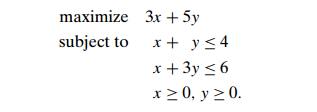
            Sketch, in the Cartesian plane, the problem’s feasible region, defined as the set of points satisfying all the problem’s constraints.

            Identify the region’s extreme points.

            Solve this optimization problem by using the following theorem: A linear programming problem with a nonempty bounded feasible region always has a solution, which can be found at one of the extreme points of its feasible region.