Brute Force and Exhaustive Search

Brute Force and Exhaustive Search

Science is as far removed from brute force as this sword from a crowbar.

—Edward Lytton (1803–1873), Leila, Book II, Chapter I

Doing a thing well is often a waste of time.

—Robert Byrne, a master pool and billiards player and a writer

Ater introducing the framework and methods for algorithm analysis in the preceding chapter, we are ready to embark on a discussion of algorithm design strategies. Each of the next eight chapters is devoted to a particular design strategy. The subject of this chapter is brute force and its important special case,

exhaustive search. Brute force can be described as follows:

Brute force is a straightforward approach to solving a problem, usually directly based on the problem statement and definitions of the concepts involved.

The “force” implied by the strategy’s definition is that of a computer and not that of one’s intellect. “Just do it!” would be another way to describe the prescription of the brute-force approach. And often, the brute-force strategy is indeed the one that is easiest to apply.

As an example, consider the exponentiation problem: compute aⁿ for a nonzero number a and a nonnegative integer n. Although this problem might seem trivial, it provides a useful vehicle for illustrating several algorithm design strategies, including the brute force. (Also note that computing aⁿ mod m for some large integers is a principal component of a leading encryption algorithm.) By the definition of exponentiation,

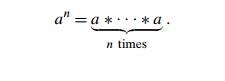
This suggests simply computing aⁿ by multiplying 1 by a n times.

We have already encountered at least two brute-force algorithms in the book: the consecutive integer checking algorithm for computing gcd(m, n) in Section 1.1 and the definition-based algorithm for matrix multiplication in Section 2.3. Many other examples are given later in this chapter. (Can you identify a few algorithms you already know as being based on the brute-force approach?)

Though rarely a source of clever or efficient algorithms, the brute-force ap-proach should not be overlooked as an important algorithm design strategy. First, unlike some of the other strategies, brute force is applicable to a very wide va-riety of problems. In fact, it seems to be the only general approach for which it is more difficult to point out problems it cannot tackle. Second, for some impor-tant problems—e.g., sorting, searching, matrix multiplication, string matching— the brute-force approach yields reasonable algorithms of at least some practi-cal value with no limitation on instance size. Third, the expense of designing a more efficient algorithm may be unjustifiable if only a few instances of a prob-lem need to be solved and a brute-force algorithm can solve those instances with acceptable speed. Fourth, even if too inefficient in general, a brute-force algo-rithm can still be useful for solving small-size instances of a problem. Finally, a brute-force algorithm can serve an important theoretical or educational pur-pose as a yardstick with which to judge more efficient alternatives for solving a problem.