Chapter: Introduction to the Design and Analysis of Algorithms : Brute Force and Exhaustive Search
Sequential Search and Brute-Force String Matching
Sequential
Search and Brute-Force String Matching
We saw in
the previous section two applications of the brute-force approach to the sorting
porblem. Here we discuss two applications of this strategy to the problem of
searching. The first deals with the canonical problem of searching for an item
of a given value in a given list. The second is different in that it deals with
the string-matching problem.
We have
already encountered a brute-force algorithm for the general searching problem:
it is called sequential search (see Section 2.1). To repeat, the algorithm
simply compares successive elements of a given list with a given search key
until either a match is encountered (successful search) or the list is
exhausted without finding a match (unsuccessful search). A simple extra trick
is often employed in implementing sequential search: if we append the search
key to the end of the list, the search for the key will have to be successful,
and therefore we can eliminate the end of list check altogether. Here is
pseudocode of this enhanced version.
ALGORITHM SequentialSearch2(A[0..n],
K)
//Implements
sequential search with a search key as a sentinel //Input: An array A of n elements
and a search key K
//Output:
The index of the first element in A[0..n − 1] whose
value is
equal to K or −1 if no such element is found
A[n] ← K i ← 0
while A[i] = K do i ← i + 1
if i < n return i else return −1
Another
straightforward improvement can be incorporated in sequential search if a given
list is known to be sorted: searching in such a list can be stopped as soon as
an element greater than or equal to the search key is encountered.
Sequential
search provides an excellent illustration of the brute-force ap-proach, with
its characteristic strength (simplicity) and weakness (inferior effi-ciency).
The efficiency results obtained in Section 2.1 for the standard version of
sequential search change for the enhanced version only very slightly, so that
the algorithm remains linear in both the worst and average cases. We discuss
later in the book several searching algorithms with a better time efficiency.
Sequential
Search and Brute-Force String Matching
Brute-Force
String Matching
Recall
the string-matching problem introduced in Section 1.3: given a string of n characters called the text
and a string of m
characters (m ≤ n) called the pattern, find a substring
of the text that matches the pattern. To put it more precisely, we want to find
i—the index of the leftmost
character of the first matching substring in the text
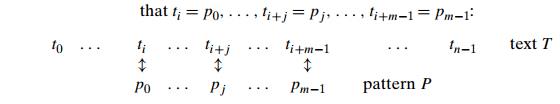
If
matches other than the first one need to be found, a string-matching algorithm
can simply continue working until the entire text is exhausted.
A
brute-force algorithm for the string-matching problem is quite obvious: align
the pattern against the first m
characters of the text and start matching the corresponding pairs of characters
from left to right until either all the m pairs of
the characters match (then the algorithm can stop) or a mismatching pair is
encountered. In the latter case, shift the pattern one position to the right
and resume the character comparisons, starting again with the first character
of the pattern and its counterpart in the text. Note that the last position in
the text that can still be a beginning of a matching substring is n − m (provided the text positions are
indexed from 0 to n − 1). Beyond that position, there
are not enough characters to match the entire pattern; hence, the algorithm
need not make any comparisons there.
ALGORITHM BruteForceStringMatch(T [0..n − 1], P [0..m − 1])
//Implements
brute-force string matching
//Input:
An array T [0..n − 1] of n characters representing a text
and
an array P [0..m − 1] of m characters representing a
pattern //Output: The index of the first character in the text that starts a
matching substring or −1 if the search is unsuccessful
for i ← 0 to n − m do j ← 0
while j
< m and P [j ] = T [i + j ] do j ← j + 1
if j = m return i return −1
An
operation of the algorithm is illustrated in Figure 3.3. Note that for this
example, the algorithm shifts the pattern almost always after a single
character comparison. The worst case is much worse: the algorithm may have to
make all m comparisons before shifting the
pattern, and this can happen for each of the n − m + 1 tries. (Problem 6 in this
section’s exercises asks you to give a specific example of such a situation.)
Thus, in the worst case, the algorithm makes

FIGURE 3.3
Example of brute-force string matching. The
pattern’s characters that are compared
with their text counterparts are in bold type.
m(n − m + 1) character comparisons, which puts
it in the O(nm) class. For a typical word search in a natural language
text, however, we should expect that most shifts would happen after very few
comparisons (check the example again). Therefore, the average-case efficiency
should be considerably better than the worst-case efficiency. Indeed it is: for
searching in random texts, it has been shown to be linear, i.e., (n). There
are several more sophisticated and more efficient algorithms for string
searching. The most widely known of them—by R. Boyer and J. Moore—is outlined
in Section 7.2 along with its simplification suggested by R. Horspool.
Exercises
3.2
Find the
number of comparisons made by the sentinel version of sequential search in the
worst case.
in the
average case if the probability of a successful search is p (0 ≤ p ≤ 1).
As shown
in Section 2.1, the average number of key comparisons made by sequential search
(without a sentinel, under standard assumptions about its inputs) is given by
the formula
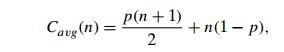
where p is the probability of a
successful search. Determine, for a fixed n, the
values of p (0 ≤ p ≤ 1) for which this formula yields
the maximum value of Cavg(n)
and the
minimum value of Cavg(n).
Gadget testing A firm wants to determine the
highest floor of its n-story headquarters from which a gadget can fall without breaking. The
firm has two identical gadgets to experiment with. If one of them gets broken,
it cannot be repaired, and the experiment will have to be completed with the
remaining gadget. Design an algorithm in the best efficiency class you can to
solve this problem.
Determine the number of character comparisons made
by the brute-force algorithm in searching for the pattern GANDHI in the
text
THERE_IS_MORE_TO_LIFE_THAN_INCREASING_ITS_SPEED
Assume
that the length of the text—it is 47 characters long—is known before the search
starts.
How many comparisons (both successful and
unsuccessful) will be made by the brute-force algorithm in searching for each
of the following patterns in the binary text of one thousand zeros?
a. 00001 b. 10000 c. 01010
Give an example of a text of length n and a pattern of length m that constitutes a worst-case
input for the brute-force string-matching algorithm. Exactly how many character
comparisons will be made for such input?
In solving the string-matching problem, would there
be any advantage in comparing pattern and text characters right-to-left instead
of left-to-right?
Consider the problem of counting, in a given text,
the number of substrings that start with an A and end with a B. For example, there are four such substrings in CABAAXBYA.
Design a brute-force algorithm for this problem and
determine its effi-ciency class.
Design a more efficient algorithm for this problem.
[Gin04]
Write a visualization program for the brute-force
string-matching algorithm.
Word Find
A popular
diversion in the United States, “word find” (or “word search”) puzzles ask the player to find each of a given set of
words in a square table filled with single letters. A word can read
horizontally (left or right), vertically (up or down), or along a 45 degree
diagonal (in any of the four directions) formed by consecutively adjacent cells
of the table; it may wrap around the table’s boundaries, but it must read in
the same direction with no zigzagging. The same cell of the table may be used
in different words, but, in a given word, the same cell may be used no more
than once. Write a computer program for solving this puzzle.
Related Topics