Exhaustive Search

Exhaustive Search

Exhaustive Search:

1. Traveling Salesman Problem

2. Knapsack Problem

3. Assignment Problem

4. Exercises

Many important problems require finding an element with a special property in a domain that grows exponentially (or faster) with an instance size. Typically, such problems arise in situations that involve—explicitly or implicitly—combinatorial objects such as permutations, combinations, and subsets of a given set. Many such problems are optimization problems: they ask to find an element that maximizes or minimizes some desired characteristic such as a path length or an assignment cost.

Exhaustive search is simply a brute-force approach to combinatorial prob-lems. It suggests generating each and every element of the problem domain, se-lecting those of them that satisfy all the constraints, and then finding a desired element (e.g., the one that optimizes some objective function). Note that although the idea of exhaustive search is quite straightforward, its implementation typically requires an algorithm for generating certain combinatorial objects. We delay a dis-cussion of such algorithms until the next chapter and assume here that they exist.

We illustrate exhaustive search by applying it to three important problems: the traveling salesman problem, the knapsack problem, and the assignment problem.

Traveling Salesman Problem

The traveling salesman problem (TSP) has been intriguing researchers for the last 150 years by its seemingly simple formulation, important applications, and interesting connections to other combinatorial problems. In layman’s terms, the problem asks to find the shortest tour through a given set of n cities that visits each city exactly once before returning to the city where it started. The problem can be conveniently modeled by a weighted graph, with the graph’s vertices representing the cities and the edge weights specifying the distances. Then the problem can be stated as the problem of finding the shortest Hamiltonian circuit of the graph. (A Hamiltonian circuit is defined as a cycle that passes through all the vertices of the graph exactly once. It is named after the Irish mathematician Sir William Rowan Hamilton (1805–1865), who became interested in such cycles as an application of his algebraic discoveries.)

It is easy to see that a Hamiltonian circuit can also be defined as a sequence of n + 1 adjacent vertices v_i0 , v_i1, . . . , v_in−1, v_i0 , where the first vertex of the sequence is the same as the last one and all the other n − 1 vertices are distinct. Further, we can assume, with no loss of generality, that all circuits start and end at one particular vertex (they are cycles after all, are they not?). 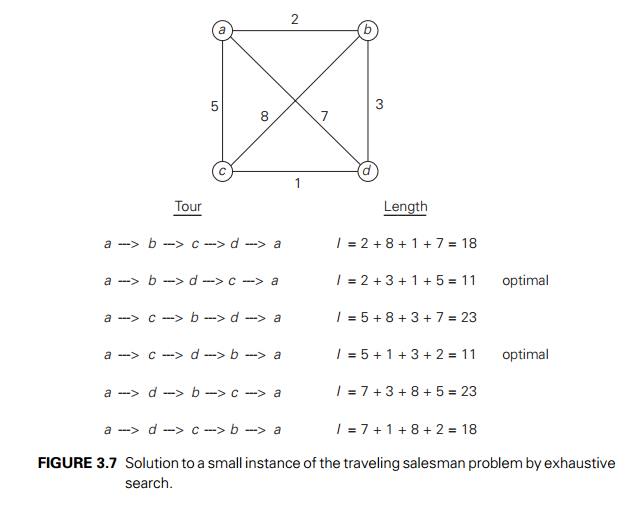Thus, we can get all the tours by generating all the permutations of n − 1 intermediate cities, compute the tour lengths, and find the shortest among them. Figure 3.7 presents a small instance of the problem and its solution by this method.

An inspection of Figure 3.7 reveals three pairs of tours that differ only by their direction. Hence, we could cut the number of vertex permutations by half. We could, for example, choose any two intermediate vertices, say, b and c, and then consider only permutations in which b precedes c. (This trick implicitly defines a tour’s direction.)

This improvement cannot brighten the efficiency picture much, however. The total number of permutations needed is still ₂¹ (n − 1)!, which makes the exhaustive-search approach impractical for all but very small values of n. On the other hand, if you always see your glass as half-full, you can claim that cutting the work by half is nothing to sneeze at, even if you solve a small instance of the problem, especially by hand. Also note that had we not limited our investigation to the circuits starting at the same vertex, the number of permutations would have been even larger, by a factor of n.

Knapsack Problem

Here is another well-known problem in algorithmics. Given n items of known weights w₁, w₂, . . . , w_n and values v₁, v₂, . . . , v_n and a knapsack of capacity W , find the most valuable subset of the items that fit into the knapsack. If you do not like the idea of putting yourself in the shoes of a thief who wants to steal the most

valuable loot that fits into his knapsack, think about a transport plane that has to deliver the most valuable set of items to a remote location without exceeding the plane’s capacity. Figure 3.8a presents a small instance of the knapsack problem.

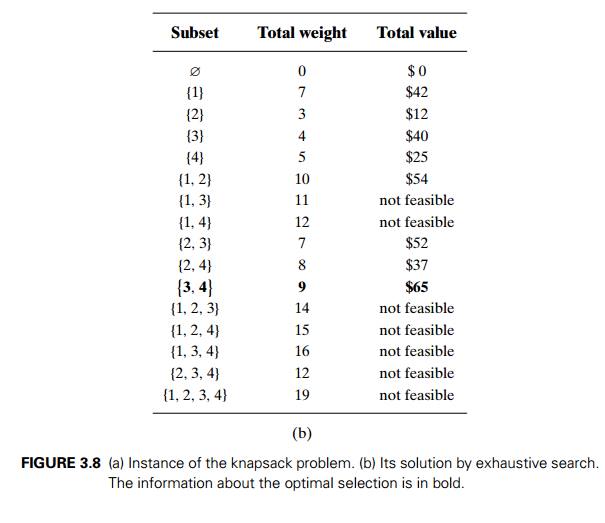
The exhaustive-search approach to this problem leads to generating all the subsets of the set of n items given, computing the total weight of each subset in order to identify feasible subsets (i.e., the ones with the total weight not exceeding the knapsack capacity), and finding a subset of the largest value among them. As an example, the solution to the instance of Figure 3.8a is given in Figure 3.8b. Since the number of subsets of an n-element set is 2ⁿ, the exhaustive search leads to a  (2ⁿ) algorithm, no matter how efficiently individual subsets are generated.

Thus, for both the traveling salesman and knapsack problems considered above, exhaustive search leads to algorithms that are extremely inefficient on every input. In fact, these two problems are the best-known examples of so-called NP-hard problems. No polynomial-time algorithm is known for any NP-hard problem. Moreover, most computer scientists believe that such algorithms do not exist, although this very important conjecture has never been proven. More-sophisticated approaches—backtracking and branch-and-bound (see Sec-tions 12.1 and 12.2)—enable us to solve some but not all instances of these and

similar problems in less than exponential time. Alternatively, we can use one of many approximation algorithms, such as those described in Section 12.3.

Assignment Problem

In our third example of a problem that can be solved by exhaustive search, there are n people who need to be assigned to execute n jobs, one person per job. (That is, each person is assigned to exactly one job and each job is assigned to exactly one person.) The cost that would accrue if the ith person is assigned to the j th job is a known quantity C[i, j ] for each pair i, j = 1, 2, . . . , n. The problem is to find an assignment with the minimum total cost.

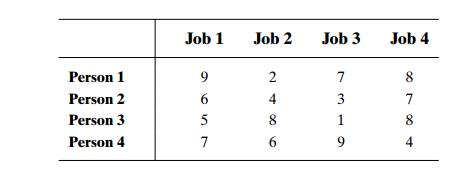
A small instance of this problem follows, with the table entries representing the assignment costs C[i, j ]:

It is easy to see that an instance of the assignment problem is completely specified by its cost matrix C. In terms of this matrix, the problem is to select one element in each row of the matrix so that all selected elements are in different columns and the total sum of the selected elements is the smallest possible. Note that no obvious strategy for finding a solution works here. For example, we cannot select the smallest element in each row, because the smallest elements may happen to be in the same column. In fact, the smallest element in the entire matrix need not be a component of an optimal solution. Thus, opting for the exhaustive search may appear as an unavoidable evil.

We can describe feasible solutions to the assignment problem as n-tuples j₁, . . . , j_n in which the ith component, i = 1, . . . , n, indicates the column of the element selected in the ith row (i.e., the job number assigned to the ith person). For example, for the cost matrix above, 2, 3, 4, 1 indicates the assignment of Person 1 to Job 2, Person 2 to Job 3, Person 3 to Job 4, and Person 4 to Job 1. The requirements of the assignment problem imply that there is a one-to-one correspondence between feasible assignments and permutations of the first n integers. Therefore, the exhaustive-search approach to the assignment problem would require generating all the permutations of integers 1, 2, . . . , n, computing the total cost of each assignment by summing up the corresponding elements of the cost matrix, and finally selecting the one with the smallest sum. A few first iterations of applying this algorithm to the instance given above are shown in Figure 3.9; you are asked to complete it in the exercises.

Since the number of permutations to be considered for the general case of the assignment problem is n!, exhaustive search is impractical for all but very small instances of the problem. Fortunately, there is a much more efficient algorithm for this problem called the Hungarian method after the Hungarian mathematicians Konig¨ and Egervary,´ whose work underlies the method (see, e.g., [Kol95]).

This is good news: the fact that a problem domain grows exponentially or faster does not necessarily imply that there can be no efficient algorithm for solving it. In fact, we present several other examples of such problems later in the book. However, such examples are more of an exception to the rule. More often than not, there are no known polynomial-time algorithms for problems whose domain grows exponentially with instance size, provided we want to solve them exactly. And, as we mentioned above, such algorithms quite possibly do not exist.

Exercises 3.4

            1. a. Assuming that each tour can be generated in constant time, what will be the efficiency class of the exhaustive-search algorithm outlined in the text for the traveling salesman problem?

            b. If this algorithm is programmed on a computer that makes ten billion additions per second, estimate the maximum number of cities for which the problem can be solved in

i. 1 hour.              ii. 24 hours.                iii. 1 year.       iv. 1 century.

           2. Outline an exhaustive-search algorithm for the Hamiltonian circuit problem.

    3.         Outline an algorithm to determine whether a connected graph represented by its adjacency matrix has an Eulerian circuit. What is the efficiency class of your algorithm?

    4.         Complete the application of exhaustive search to the instance of the assign-ment problem started in the text.

5. Give an example of the assignment problem whose optimal solution does not include the smallest element of its cost matrix.

            6. Consider the partition problem: given n positive integers, partition them into two disjoint subsets with the same sum of their elements. (Of course, the prob-lem does not always have a solution.) Design an exhaustive-search algorithm for this problem. Try to minimize the number of subsets the algorithm needs to generate.

         7.    Consider the clique problem: given a graph G and a positive integer k, deter-mine whether the graph contains a clique of size k, i.e., a complete subgraph of k vertices. Design an exhaustive-search algorithm for this problem.

           8. Explain how exhaustive search can be applied to the sorting problem and determine the efficiency class of such an algorithm.

            9. Eight-queens problem Consider the classic puzzle of placing eight queens on an 8 × 8 chessboard so that no two queens are in the same row or in the same column or on the same diagonal. How many different positions are there so that

            no two queens are on the same square?

            no two queens are in the same row?

            no two queens are in the same row or in the same column?

Also estimate how long it would take to find all the solutions to the problem by exhaustive search based on each of these approaches on a computer capable of checking 10 billion positions per second.

      10.       Magic squares A magic square of order n is an arrangement of the integers from 1 to n² in an n × n matrix, with each number occurring exactly once, so that each row, each column, and each main diagonal has the same sum.

            Prove that if a magic square of order n exists, the sum in question must be equal to n(n² + 1)/2.

            Design an exhaustive-search algorithm for generating all magic squares of order n.

            Go to the Internet or your library and find a better algorithm for generating magic squares.

            Implement the two algorithms—the exhaustive search and the one you have found—and run an experiment to determine the largest value of n for which each of the algorithms is able to find a magic square of order n in less than 1 minute on your computer.

11. Famous alphametic A puzzle in which the digits in a correct mathematical expression, such as a sum, are replaced by letters is called cryptarithm; if, in addition, the puzzle’s words make sense, it is said to be an alphametic. The most well-known alphametic was published by the renowned British puzzlist Henry E. Dudeney (1857–1930):

Two conditions are assumed: first, the correspondence between letters and decimal digits is one-to-one, i.e., each letter represents one digit only and dif-ferent letters represent different digits. Second, the digit zero does not appear as the left-most digit in any of the numbers. To solve an alphametic means to find which digit each letter represents. Note that a solution’s uniqueness cannot be assumed and has to be verified by the solver.

            Write a program for solving cryptarithms by exhaustive search. Assume that a given cryptarithm is a sum of two words.