Chapter: Introduction to the Design and Analysis of Algorithms
Fundamentals of Algorithmic Problem Solving
Fundamentals of
Algorithmic Problem Solving
Let us start by reiterating an important point
made in the introduction to this chapter:
We can consider algorithms to be procedural solutions
to problems.
These solutions are not answers but specific
instructions for getting answers. It is this emphasis on precisely defined
constructive procedures that makes computer science distinct from other
disciplines. In particular, this distinguishes it from the-oretical
mathematics, whose practitioners are typically satisfied with just proving the
existence of a solution to a problem and, possibly, investigating the
solutionŌĆÖs properties.
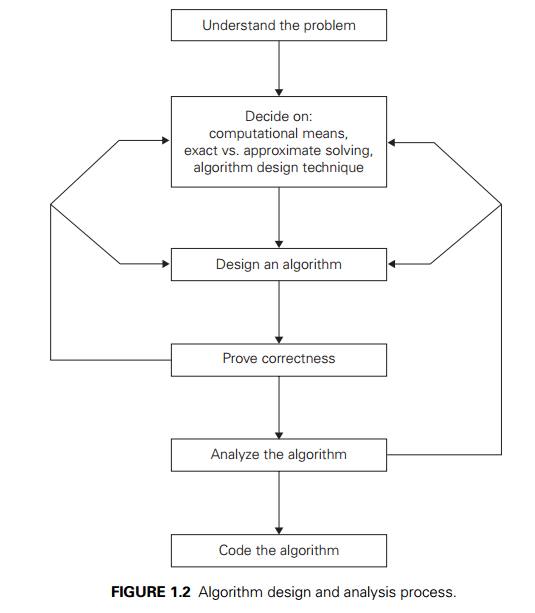
We now list and briefly discuss a sequence of
steps one typically goes through in designing and analyzing an algorithm
(Figure 1.2).
Understanding the Problem
From a practical perspective, the first thing
you need to do before designing an algorithm is to understand completely the
problem given. Read the problemŌĆÖs description carefully and ask questions if
you have any doubts about the problem, do a few small examples by hand, think
about special cases, and ask questions again if needed.
There are a few types of problems that arise in
computing applications quite often. We review them in the next section. If the
problem in question is one of them, you might be able to use a known algorithm
for solving it. Of course, it helps to understand how such an algorithm works
and to know its strengths and weaknesses, especially if you have to choose
among several available algorithms. But often you will not find a readily
available algorithm and will have to design your own. The sequence of steps
outlined in this section should help you in this exciting but not always easy
task.
An input to an algorithm specifies an instance
of the problem the algorithm solves. It is very important to specify exactly
the set of instances the algorithm needs to handle. (As an example, recall the
variations in the set of instances for the three greatest common divisor
algorithms discussed in the previous section.) If you fail to do this, your
algorithm may work correctly for a majority of inputs but crash on some
ŌĆ£boundaryŌĆØ value. Remember that a correct algorithm is not one that works most
of the time, but one that works correctly for all legitimate inputs.
Do not skimp on this first step of the
algorithmic problem-solving process; otherwise, you will run the risk of
unnecessary rework.
Ascertaining the Capabilities
of the Computational Device
Once you completely understand a problem, you
need to ascertain the capabilities of the computational device the algorithm is
intended for. The vast majority of
algorithms in use today are still destined to
be programmed for a computer closely resembling the von Neumann machineŌĆöa
computer architecture outlined by the prominent Hungarian-American
mathematician John von Neumann (1903ŌĆō 1957), in collaboration with A. Burks and
H. Goldstine, in 1946. The essence of this architecture is captured by the
so-called random-access machine (RAM). Its central assumption is that
instructions are executed one after another, one operation at a time.
Accordingly, algorithms designed to be executed on such machines are called sequential
algorithms.
The central assumption of the RAM model does
not hold for some newer computers that can execute operations concurrently,
i.e., in parallel. Algorithms that take advantage of this capability are called
parallel
algorithms. Still, studying the classic techniques for design and
analysis of algorithms under the RAM model remains the cornerstone of
algorithmics for the foreseeable future.
Should you worry about the speed and amount of
memory of a computer at your disposal? If you are designing an algorithm as a
scientific exercise, the answer is a qualified no. As you will see in Section
2.1, most computer scientists prefer to study algorithms in terms independent
of specification parameters for a particular computer. If you are designing an
algorithm as a practical tool, the answer may depend on a problem you need to
solve. Even the ŌĆ£slowŌĆØ computers of today are almost unimaginably fast.
Consequently, in many situations you need not worry about a computer being too
slow for the task. There are important problems, however, that are very complex
by their nature, or have to process huge volumes of data, or deal with
applications where the time is critical. In such situations, it is imperative
to be aware of the speed and memory available on a particular computer system.
Choosing between Exact and
Approximate Problem Solving
The next principal decision is to choose
between solving the problem exactly or solving it approximately. In the former
case, an algorithm is called an exact algo-rithm; in the latter
case, an algorithm is called an approximation algorithm. Why would
one opt for an approximation algorithm? First, there are important prob-lems
that simply cannot be solved exactly for most of their instances; examples
include extracting square roots, solving nonlinear equations, and evaluating
def-inite integrals. Second, available algorithms for solving a problem exactly
can be unacceptably slow because of the problemŌĆÖs intrinsic complexity. This
happens, in particular, for many problems involving a very large number of
choices; you will see examples of such difficult problems in Chapters 3, 11,
and 12. Third, an ap-proximation algorithm can be a part of a more
sophisticated algorithm that solves a problem exactly.
Algorithm Design Techniques
Now, with all the components of the algorithmic
problem solving in place, how do you design an algorithm to solve a given
problem? This is the main question this book seeks to answer by teaching you
several general design techniques.
What is an algorithm design technique?
An algorithm design technique (or
ŌĆ£strategyŌĆØ or ŌĆ£paradigmŌĆØ) is a general approach to solving problems
algorithmically that is applicable to a variety of problems from different
areas of computing.
Check this bookŌĆÖs table of contents and you
will see that a majority of its chapters are devoted to individual design
techniques. They distill a few key ideas that have proven to be useful in
designing algorithms. Learning these techniques is of utmost importance for the
following reasons.
First, they provide guidance for designing
algorithms for new problems, i.e., problems for which there is no known
satisfactory algorithm. ThereforeŌĆöto use the language of a famous
proverbŌĆölearning such techniques is akin to learning to fish as opposed to being
given a fish caught by somebody else. It is not true, of course, that each of
these general techniques will be necessarily applicable to every problem you
may encounter. But taken together, they do constitute a powerful collection of
tools that you will find quite handy in your studies and work.
Second, algorithms are the cornerstone of
computer science. Every science is interested in classifying its principal
subject, and computer science is no exception. Algorithm design techniques make
it possible to classify algorithms according to an underlying design idea;
therefore, they can serve as a natural way to both categorize and study
algorithms.
Designing an Algorithm and
Data Structures
While the algorithm design techniques do provide
a powerful set of general ap-proaches to algorithmic problem solving, designing
an algorithm for a particular problem may still be a challenging task. Some
design techniques can be simply inapplicable to the problem in question.
Sometimes, several techniques need to be combined, and there are algorithms
that are hard to pinpoint as applications of the known design techniques. Even
when a particular design technique is ap-plicable, getting an algorithm often
requires a nontrivial ingenuity on the part of the algorithm designer. With
practice, both tasksŌĆöchoosing among the general techniques and applying
themŌĆöget easier, but they are rarely easy.
Of course, one should pay close attention to
choosing data structures appro-priate for the operations performed by the
algorithm. For example, the sieve of Eratosthenes introduced in Section 1.1
would run longer if we used a linked list instead of an array in its
implementation (why?). Also note that some of the al-gorithm design techniques
discussed in Chapters 6 and 7 depend intimately on structuring or restructuring
data specifying a problemŌĆÖs instance. Many years ago, an influential textbook
proclaimed the fundamental importance of both algo-rithms and data structures
for computer programming by its very title: Algorithms
+ Data Structures = Programs [Wir76].
In the new world of object-oriented programming, data structures remain
crucially important for both design and analysis of algorithms. We review basic
data structures in Section 1.4.
Methods of Specifying an
Algorithm
Once you have designed an algorithm, you need
to specify it in some fashion. In Section 1.1, to give you an example, EuclidŌĆÖs
algorithm is described in words (in a free and also a step-by-step form) and in
pseudocode. These are the two options that are most widely used nowadays for
specifying algorithms.
Using a natural language has an obvious appeal;
however, the inherent ambi-guity of any natural language makes a succinct and
clear description of algorithms surprisingly difficult. Nevertheless, being
able to do this is an important skill that you should strive to develop in the
process of learning algorithms.
Pseudocode is a mixture of a natural language and
programming language-like constructs. Pseudocode is usually more precise than
natural language, and its usage often yields more succinct algorithm
descriptions. Surprisingly, computer scientists have never agreed on a single
form of pseudocode, leaving textbook authors with a need to design their own
ŌĆ£dialects.ŌĆØ Fortunately, these dialects are so close to each other that anyone
familiar with a modern programming language should be able to understand them
all.
This bookŌĆÖs dialect was selected to cause
minimal difficulty for a reader. For the sake of simplicity, we omit
declarations of variables and use indentation to show the scope of such
statements as for, if, and while. As you saw in the previous section, we use an arrow ŌĆ£ŌåÉŌĆØ for the assignment operation and two slashes ŌĆ£//ŌĆØ for comments.
In the earlier days of computing, the dominant
vehicle for specifying algo-rithms was a flowchart, a method of expressing an
algorithm by a collection of connected geometric shapes containing descriptions
of the algorithmŌĆÖs steps. This representation technique has proved to be
inconvenient for all but very simple algorithms; nowadays, it can be found only
in old algorithm books.
The state of the art of computing has not yet
reached a point where an algorithmŌĆÖs descriptionŌĆöbe it in a natural language or
pseudocodeŌĆöcan be fed into an electronic computer directly. Instead, it needs
to be converted into a computer program written in a particular computer
language. We can look at such a program as yet another way of specifying the
algorithm, although it is preferable to consider it as the algorithmŌĆÖs
implementation.
Proving an AlgorithmŌĆÖs
Correctness
Once an algorithm has been specified, you have
to prove its correctness. That is, you have to prove that the algorithm
yields a required result for every legitimate input in a finite amount of time.
For example, the correctness of EuclidŌĆÖs algorithm for computing the greatest
common divisor stems from the correctness of the equality gcd(m, n) = gcd(n, m mod n) (which, in turn, needs a proof; see Problem 7
in Exercises 1.1), the simple observation that the second integer gets smaller
on every iteration of the algorithm, and the fact that the algorithm stops when
the second integer becomes 0.
For some algorithms, a proof of correctness is
quite easy; for others, it can be quite complex. A common technique for proving
correctness is to use mathemati-cal induction because an algorithmŌĆÖs iterations
provide a natural sequence of steps needed for such proofs. It might be worth
mentioning that although tracing the algorithmŌĆÖs performance for a few specific
inputs can be a very worthwhile activ-ity, it cannot prove the algorithmŌĆÖs
correctness conclusively. But in order to show that an algorithm is incorrect,
you need just one instance of its input for which the algorithm fails.
The notion of correctness for approximation
algorithms is less straightforward than it is for exact algorithms. For an
approximation algorithm, we usually would like to be able to show that the
error produced by the algorithm does not exceed a predefined limit. You can
find examples of such investigations in Chapter 12.
Analyzing an Algorithm
We usually want our algorithms to possess
several qualities. After correctness, by far the most important is efficiency.
In fact, there are two kinds of algorithm efficiency: time efficiency,
indicating how fast the algorithm runs, and space ef-ficiency,
indicating how much extra memory it uses. A general framework and specific
techniques for analyzing an algorithmŌĆÖs efficiency appear in Chapter 2.
Another desirable characteristic of an
algorithm is simplicity. Unlike effi-ciency, which can be precisely defined
and investigated with mathematical rigor, simplicity, like beauty, is to a
considerable degree in the eye of the beholder. For example, most people would
agree that EuclidŌĆÖs algorithm is simpler than the middle-school procedure for
computing gcd(m, n), but it is not clear whether Eu-clidŌĆÖs algorithm is simpler than
the consecutive integer checking algorithm. Still, simplicity is an important
algorithm characteristic to strive for. Why? Because sim-pler algorithms are
easier to understand and easier to program; consequently, the resulting
programs usually contain fewer bugs. There is also the undeniable aes-thetic
appeal of simplicity. Sometimes simpler algorithms are also more efficient than
more complicated alternatives. Unfortunately, it is not always true, in which
case a judicious compromise needs to be made.
Yet another desirable characteristic of an
algorithm is generality. There are, in fact, two issues here: generality of
the problem the algorithm solves and the set of inputs it accepts. On the first
issue, note that it is sometimes easier to design an algorithm for a problem
posed in more general terms. Consider, for example, the problem of determining
whether two integers are relatively prime, i.e., whether their only common
divisor is equal to 1. It is easier to design an algorithm for a more general
problem of computing the greatest common divisor of two integers and, to solve
the former problem, check whether the gcd is 1 or not. There are situations,
however, where designing a more general algorithm is unnecessary or difficult
or even impossible. For example, it is unnecessary to sort a list of n numbers to find its median, which is its n/2 th smallest element. To give another example, the standard
formula for roots of a quadratic equation cannot be generalized to handle
polynomials of arbitrary degrees.
As to the set of inputs, your main concern
should be designing an algorithm that can handle a set of inputs that is
natural for the problem at hand. For example, excluding integers equal to 1 as
possible inputs for a greatest common divisor algorithm would be quite
unnatural. On the other hand, although the standard formula for the roots of a
quadratic equation holds for complex coefficients, we would normally not
implement it on this level of generality unless this capability is explicitly
required.
If you are not satisfied with the algorithmŌĆÖs
efficiency, simplicity, or generality, you must return to the drawing board and
redesign the algorithm. In fact, even if your evaluation is positive, it is
still worth searching for other algorithmic solutions. Recall the three
different algorithms in the previous section for computing the greatest common
divisor: generally, you should not expect to get the best algorithm on the
first try. At the very least, you should try to fine-tune the algorithm you
already have. For example, we made several improvements in our implementation
of the sieve of Eratosthenes compared with its initial outline in Section 1.1.
(Can you identify them?) You will do well if you keep in mind the following
observation of Antoine de Saint-Exupery,┬┤ the French writer, pilot, and
aircraft designer: ŌĆ£A designer knows he has arrived at perfection not when
there is no longer anything to add, but when there is no longer anything to
take away.ŌĆØ1
Coding an Algorithm
As a practical matter, the validity of programs
is still established by testing. Testing of computer programs is an art rather
than a science, but that does not mean that there is nothing in it to learn.
Look up books devoted to testing and debugging; even more important, test and
debug your program thoroughly whenever you implement an algorithm.
Also note that throughout the book, we assume that
inputs to algorithms belong to the specified sets and hence require no
verification. When implementing algorithms as programs to be used in actual
applications, you should provide such verifications.
Of course, implementing an algorithm correctly
is necessary but not sufficient: you would not like to diminish your
algorithmŌĆÖs power by an inefficient implemen-tation. Modern compilers do
provide a certain safety net in this regard, especially when they are used in
their code optimization mode. Still, you need to be aware of such standard
tricks as computing a loopŌĆÖs invariant (an expression that does not change its
value) outside the loop, collecting common subexpressions, replac-ing expensive
operations by cheap ones, and so on. (See [Ker99] and [Ben00] for a good
discussion of code tuning and other issues related to algorithm program-ming.)
Typically, such improvements can speed up a program only by a constant factor,
whereas a better algorithm can make a difference in running time by orders of
magnitude. But once an algorithm is selected, a 10ŌĆō50% speedup may be worth an
effort.
A working program provides an additional
opportunity in allowing an em-pirical analysis of the underlying algorithm.
Such an analysis is based on timing the program on several inputs and then
analyzing the results obtained. We dis-cuss the advantages and disadvantages of
this approach to analyzing algorithms in Section 2.6.
In conclusion, let us emphasize again the main
lesson of the process depicted in Figure 1.2:
As a rule, a good algorithm is a result of
repeated effort and rework.
Even if you have been fortunate enough to get
an algorithmic idea that seems perfect, you should still try to see whether it
can be improved.
Actually, this is good news since it makes the
ultimate result so much more enjoyable. (Yes, I did think of naming this book The Joy of Algorithms.) On the other
hand, how does one know when to stop? In the real world, more often than not a
projectŌĆÖs schedule or the impatience of your boss will stop you. And so it
should be: perfection is expensive and in fact not always called for. Designing
an algorithm is an engineering-like activity that calls for compromises among
competing goals under the constraints of available resources, with the
designerŌĆÖs time being one of the resources.
In the academic world, the question leads to an
interesting but usually difficult investigation of an algorithmŌĆÖs optimality.
Actually, this question is not about the efficiency of an algorithm but about
the complexity of the problem it solves: What is the minimum amount of effort any algorithm will need to exert to
solve the problem? For some problems, the answer to this question is known. For
example, any algorithm that sorts an array by comparing values of its elements
needs about n log2 n comparisons for some arrays of size n (see Section 11.2). But for many seemingly easy problems such as integer
multiplication, computer scientists do not yet have a final answer.
Another important issue of algorithmic problem
solving is the question of whether or not every problem can be solved by an
algorithm. We are not talking here about problems that do not have a solution,
such as finding real roots of a quadratic equation with a negative
discriminant. For such cases, an output indicating that the problem does not
have a solution is all we can and should expect from an algorithm. Nor are we
talking about ambiguously stated problems. Even some unambiguous problems that
must have a simple yes or no answer are ŌĆ£undecidable,ŌĆØ i.e., unsolvable by any
algorithm. An important example of such a problem appears in Section 11.3.
Fortunately, a vast majority of problems in practical computing can be solved by an algorithm.
Before leaving this section, let us be sure
that you do not have the misconceptionŌĆöpossibly caused by the somewhat
mechanical nature of the diagram of Figure 1.2ŌĆöthat designing an algorithm is a
dull activity. There is nothing further from the truth: inventing (or
discovering?) algorithms is a very creative and rewarding process. This book is
designed to convince you that this is the case.
Exercises
1.2
Old World puzzle A peasant finds himself on a riverbank with a
wolf, a goat, and a head of cabbage.
He needs to transport all three to the other side of the river in his boat.
However, the boat has room for only the peasant himself and one other item
(either the wolf, the goat, or the cabbage). In his absence, the wolf would eat
the goat, and the goat would eat the cabbage. Solve this problem for the
peasant or prove it has no solution. (Note: The peasant is a vegetarian but
does not like cabbage and hence can eat neither the goat nor the cabbage to
help him solve the problem. And it goes without saying that the wolf is a
protected species.)
New World puzzle There are four people who want to cross a
rickety bridge; they all begin on the
same side. You have 17 minutes to get them all across to the other side. It is
night, and they have one flashlight. A maximum of two people can cross the
bridge at one time. Any party that crosses, either one or two people, must have
the flashlight with them. The flashlight must be walked back and forth; it
cannot be thrown, for example. Person 1 takes 1 minute to cross the bridge,
person 2 takes 2 minutes, person 3 takes 5 minutes, and person 4 takes 10 minutes.
A pair must walk together at the rate of the slower personŌĆÖs pace. (Note:
According to a rumor on the Internet, interviewers at a well-known software
company located near Seattle have given this problem to interviewees.)
Which of
the following formulas can be considered an algorithm for comput-ing the area
of a triangle whose side lengths are given positive numbers a, b, and c?
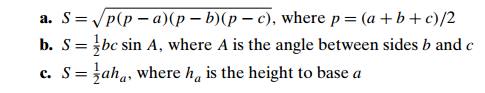
Write
pseudocode for an algorithm for finding real roots of equation ax2 + bx + c = 0 for arbitrary real coefficients a, b, and c. (You may assume the availability of the square root function sqrt (x).)
Describe
the standard algorithm for finding the binary representation of a positive
decimal integer
in
English.
in
pseudocode.
Describe
the algorithm used by your favorite ATM machine in dispensing cash. (You may
give your description in either English or pseudocode, which-ever you find more
convenient.)
a. Can the problem of computing the number ŽĆ be solved exactly?
How many
instances does this problem have?
Look up an algorithm for this problem on the
Internet.
Give an
example of a problem other than computing the greatest common divisor for which
you know more than one algorithm. Which of them is simpler? Which is more
efficient?
Consider
the following algorithm for finding the distance between the two closest
elements in an array of numbers.
ALGORITHM MinDistance(A[0..n ŌłÆ 1])
//Input: Array A[0..n ŌłÆ 1] of numbers
//Output: Minimum distance between two of its
elements dmin ŌåÉ
Ōł×
for i ŌåÉ 0 to n ŌłÆ 1 do
for j ŌåÉ 0 to n ŌłÆ 1 do
if i = j and |A[i] ŌłÆ A[j ]| < dmin dmin ŌåÉ |A[i] ŌłÆ A[j ]|
return dmin
Make as many improvements as you can in this algorithmic solution to the problem. If you need to, you may change the algorithm altogether; if not, improve the implementation given.
One of the most influential books on problem solving, titled How To Solve It [Pol57], was written by the Hungarian-American mathematician George Polya┬┤ (1887ŌĆō1985). Polya┬┤ summarized his ideas in a four-point summary. Find this summary on the Internet or, better yet, in his book, and compare it with the plan outlined in Section 1.2. What do they have in common? How are they different?
Related Topics