Chapter: Introduction to the Design and Analysis of Algorithms
Important Problem Types in Algorithms Analysis
Important Problem Types
In the limitless sea of problems one encounters
in computing, there are a few areas that have attracted particular attention
from researchers. By and large, their interest has been driven either by the
problemŌĆÖs practical importance or by some specific characteristics making the
problem an interesting research subject; fortunately, these two motivating
forces reinforce each other in most cases.
In this section, we are going to introduce the
most important problem types:
Sorting
Searching
String processing
Graph problems
Combinatorial problems
Geometric problems
Numerical problems
These problems are used in subsequent chapters
of the book to illustrate different algorithm design techniques and methods of
algorithm analysis.
Sorting
The sorting problem is to rearrange the
items of a given list in nondecreasing order. Of course, for this problem to be
meaningful, the nature of the list items must allow such an ordering.
(Mathematicians would say that there must exist a relation of total ordering.)
As a practical matter, we usually need to sort lists of numbers, characters
from an alphabet, character strings, and, most important, records similar to
those maintained by schools about their students, libraries about their
holdings, and companies about their employees. In the case of records, we need
to choose a piece of information to guide sorting. For example, we can choose
to sort student records in alphabetical order of names or by student number or
by student grade-point average. Such a specially chosen piece of information is
called a key. Computer scientists often talk about sorting a list of
keys even when the listŌĆÖs items are not records but, say, just integers.
Why would we want a sorted list? To begin with,
a sorted list can be a required output of a task such as ranking Internet
search results or ranking students by their GPA scores. Further, sorting makes
many questions about the list easier to answer. The most important of them is searching:
it is why dictionaries, telephone books, class lists, and so on are sorted. You
will see other examples of the usefulness of list presorting in Section 6.1. In
a similar vein, sorting is used as an auxiliary step in several important
algorithms in other areas, e.g., geometric algorithms and data compression. The
greedy approachŌĆöan important algorithm design technique discussed later in the
bookŌĆörequires a sorted input.
By now, computer scientists have discovered
dozens of different sorting algo-rithms. In fact, inventing a new sorting
algorithm has been likened to designing the proverbial mousetrap. And I am
happy to report that the hunt for a better sorting mousetrap continues. This
perseverance is admirable in view of the fol-lowing facts. On the one hand,
there are a few good sorting algorithms that sort an arbitrary array of size n using about n log2 n comparisons. On the other hand, no algorithm
that sorts by key comparisons (as opposed to, say, comparing small pieces of
keys) can do substantially better than that.
There is a reason for this embarrassment of
algorithmic riches in the land of sorting. Although some algorithms are indeed
better than others, there is no algorithm that would be the best solution in
all situations. Some of the algorithms are simple but relatively slow, while
others are faster but more complex; some work better on randomly ordered
inputs, while others do better on almost-sorted lists; some are suitable only
for lists residing in the fast memory, while others can be adapted for sorting
large files stored on a disk; and so on.
Two properties of sorting algorithms deserve
special mention. A sorting algo-rithm is called stable if it preserves
the relative order of any two equal elements in its input. In other words, if an
input list contains two equal elements in positions i and j where i <
j, then in the sorted list they
have to be in positions i and j ,
respectively, such that i < j . This property can be desirable if, for
example, we have a list of students sorted alphabetically and we want to sort
it according to student GPA: a stable algorithm will yield a list in which
students with the same GPA will still be sorted alphabetically. Generally
speaking, algorithms that can exchange keys located far apart are not stable,
but they usually work faster; you will see how this general comment applies to
important sorting algorithms later in the book.
The second notable feature of a sorting
algorithm is the amount of extra memory the algorithm requires. An algorithm is
said to be in-place if it does not require extra memory, except, possibly,
for a few memory units. There are important sorting algorithms that are
in-place and those that are not.
Searching
The searching problem deals with finding
a given value, called a search key, in a given set (or a
multiset, which permits several elements to have the same value). There are
plenty of searching algorithms to choose from. They range from the
straightforward sequential search to a spectacularly efficient but limited
binary search and algorithms based on representing the underlying set in a
different form more conducive to searching. The latter algorithms are of
particular importance for real-world applications because they are
indispensable for storing and retriev-ing information from large databases.
For searching, too, there is no single
algorithm that fits all situations best. Some algorithms work faster than
others but require more memory; some are very fast but applicable only to
sorted arrays; and so on. Unlike with sorting algorithms, there is no stability
problem, but different issues arise. Specifically, in applications where the
underlying data may change frequently relative to the number of searches,
searching has to be considered in conjunction with two other operations: an
addition to and deletion from the data set of an item. In such situations, data
structures and algorithms should be chosen to strike a balance among the
requirements of each operation. Also, organizing very large data sets for
efficient searching poses special challenges with important implications for
real-world applications.
String Processing
In recent decades, the rapid proliferation of
applications dealing with nonnumer-ical data has intensified the interest of
researchers and computing practitioners in string-handling algorithms. A string
is a sequence of characters from an alphabet. Strings of particular interest
are text strings, which comprise letters, numbers, and special characters; bit
strings, which comprise zeros and ones; and gene sequences, which can be
modeled by strings of characters from the four-character alphabet {A, C, G, T}. It
should be pointed out, however, that string-processing algorithms have been important for computer science for a long
time in conjunction with computer languages and compiling issues.
One particular problemŌĆöthat of searching for a
given word in a textŌĆöhas attracted special attention from researchers. They
call it string matching. Several algorithms that exploit the special
nature of this type of searching have been invented. We introduce one very
simple algorithm in Chapter 3 and discuss two algorithms based on a remarkable
idea by R. Boyer and J. Moore in Chapter 7.
Graph Problems
One of the oldest and most interesting areas in
algorithmics is graph algorithms. Informally, a graph can be thought of
as a collection of points called vertices, some of which are connected by line
segments called edges. (A more formal definition is given in the next section.)
Graphs are an interesting subject to study, for both theoretical and practical
reasons. Graphs can be used for modeling a wide variety of applications,
including transportation, communication, social and economic networks, project
scheduling, and games. Studying different technical and social aspects of the
Internet in particular is one of the active areas of current research involving
computer scientists, economists, and social scientists (see, e.g., [Eas10]).
Basic graph algorithms include graph-traversal
algorithms (how can one reach all the points in a network?), shortest-path
algorithms (what is the best route be-tween two cities?), and topological
sorting for graphs with directed edges (is a set of courses with their
prerequisites consistent or self-contradictory?). Fortunately, these algorithms
can be considered illustrations of general design techniques; accordingly, you
will find them in corresponding chapters of the book.
Some graph problems are computationally very
hard; the most well-known examples are the traveling salesman problem and the
graph-coloring problem. The traveling salesman problem (TSP) is
the problem of finding the shortest tour through n cities that visits every city exactly once. In
addition to obvious appli-cations involving route planning, it arises in such
modern applications as circuit board and VLSI chip fabrication, X-ray
crystallography, and genetic engineer-ing. The graph-coloring problem
seeks to assign the smallest number of colors to the vertices of a graph so
that no two adjacent vertices are the same color. This problem arises in
several applications, such as event scheduling: if the events are represented
by vertices that are connected by an edge if and only if the correspond-ing
events cannot be scheduled at the same time, a solution to the graph-coloring
problem yields an optimal schedule.
Combinatorial Problems
From a more abstract perspective, the traveling
salesman problem and the graph-coloring problem are examples of combinatorial
problems. These are problems that ask, explicitly or implicitly, to
find a combinatorial objectŌĆösuch as a permu-tation, a combination, or a
subsetŌĆöthat satisfies certain constraints. A desired combinatorial object may
also be required to have some additional property such as a maximum value or a
minimum cost.
Generally speaking, combinatorial problems are
the most difficult problems in computing, from both a theoretical and practical
standpoint. Their difficulty stems from the following facts. First, the number
of combinatorial objects typically grows extremely fast with a problemŌĆÖs size,
reaching unimaginable magnitudes even for moderate-sized instances. Second,
there are no known algorithms for solving most such problems exactly in an
acceptable amount of time. Moreover, most computer scientists believe that such
algorithms do not exist. This conjecture has been neither proved nor disproved,
and it remains the most important unresolved issue in theoretical computer
science. We discuss this topic in more detail in Section 11.3.
Some combinatorial problems can be solved by
efficient algorithms, but they should be considered fortunate exceptions to the
rule. The shortest-path problem mentioned earlier is among such exceptions.
Geometric Problems
Geometric algorithms deal with geometric objects such as points,
lines, and poly-gons. The ancient Greeks were very much interested in
developing procedures (they did not call them algorithms, of course) for
solving a variety of geometric problems, including problems of constructing
simple geometric shapesŌĆötriangles, circles, and so onŌĆöwith an unmarked ruler
and a compass. Then, for about 2000 years, intense interest in geometric
algorithms disappeared, to be resurrected in the age of computersŌĆöno more
rulers and compasses, just bits, bytes, and good old human ingenuity. Of
course, today people are interested in geometric algorithms with quite
different applications in mind, such as computer graphics, robotics, and
tomography.
We will discuss algorithms for only two classic
problems of computational geometry: the closest-pair problem and the convex-hull
problem. The closest-pair problem is self-explanatory: given n points
in the plane, find the closest pair among them. The convex-hull problem asks
to find the smallest convex polygon that would include all the points of a
given set. If you are interested in other geometric algorithms, you will find a
wealth of material in such specialized monographs as [deB10], [ORo98], and
[Pre85].
Numerical Problems
Many sophisticated algorithms have been
developed over the years in this area, and they continue to play a critical
role in many scientific and engineering applications. But in the last 30 years
or so, the computing industry has shifted its focus to business applications.
These new applications require primarily algo-rithms for information storage,
retrieval, transportation through networks, and presentation to users. As a
result of this revolutionary change, numerical analysis has lost its formerly
dominating position in both industry and computer science programs. Still, it
is important for any computer-literate person to have at least a rudimentary
idea about numerical algorithms. We discuss several classical numer-ical
algorithms in Sections 6.2, 11.4, and 12.4.
Exercises
1.3
Consider
the algorithm for the sorting problem that sorts an array by counting, for each
of its elements, the number of smaller elements and then uses this information
to put the element in its appropriate position in the sorted array:
ALGORITHM ComparisonCountingSort(A[0..n ŌłÆ 1])
//Sorts an array by comparison counting
//Input: Array A[0..n ŌłÆ 1] of orderable values
//Output: Array S[0..n ŌłÆ 1] of AŌĆÖs elements
sorted // in nondecreasing order
for i ŌåÉ 0 to n ŌłÆ 1 do
Count[i] ŌåÉ 0 for i ŌåÉ 0 to n ŌłÆ 2 do
for j ŌåÉ i + 1 to n ŌłÆ 1 do
if A[i] < A[j ]
Count[j ] ŌåÉ Count[j ] + 1 else Count[i] ŌåÉ
Count[i] + 1
for i ŌåÉ 0 to n ŌłÆ 1 do
S[Count[i]] ŌåÉ A[i] return S
Apply this algorithm to sorting the list 60,
35, 81, 98, 14, 47.
Is this algorithm stable?
Is it in-place?
Name the algorithms for the searching
problem that you already know. Give a good succinct description of each
algorithm in English. If you know no such algorithms, use this opportunity to
design one.
Design a simple algorithm for the string-matching
problem.
Konigsberg┬© bridges The Konigsberg┬© bridge
puzzle is universally accepted as the problem that gave birth to graph theory.
It was solved by the great Swiss-born mathematician Leonhard Euler (1707ŌĆō1783).
The problem asked whether one could, in a single stroll, cross all seven
bridges of the city of Konigsberg┬© exactly once and return to a starting point.
Following is a sketch of the river with its two islands and seven bridges:

State the problem as a graph problem.
Does this problem have a solution? If you
believe it does, draw such a stroll; if you believe it does not, explain why
and indicate the smallest number of new bridges that would be required to make
such a stroll possible.
Icosian Game A century after EulerŌĆÖs discovery
(see Problem 4), another famous puzzleŌĆöthis one invented by the renowned Irish
mathematician Sir William Hamilton (1805ŌĆō1865)ŌĆöwas presented to the world under
the name of the Icosian Game. The gameŌĆÖs board was a circular wooden board on
which the following graph was carved:
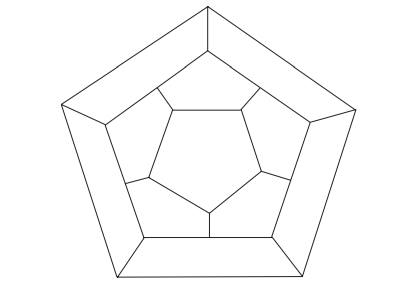
Find a Hamiltonian circuitŌĆöa path that visits
all the graphŌĆÖs vertices exactly once before returning to the starting
vertexŌĆöfor this graph.
Consider the following problem: Design an
algorithm to determine the best route for a subway passenger to take from one
designated station to another in a well-developed subway system similar to
those in such cities as Washington, D.C., and London, UK.
The
problemŌĆÖs statement is somewhat vague, which is typical of real-life problems.
In particular, what reasonable criterion can be used for defining the ŌĆ£bestŌĆØ
route?
How
would you model this problem by a graph?
a.
Rephrase the traveling-salesman problem in combinatorial object terms.
Rephrase
the graph-coloring problem in combinatorial object terms.
Consider
the following map:
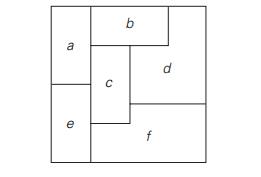
Explain
how we can use the graph-coloring problem to color the map so that no two
neighboring regions are colored the same.
Use
your answer to part (a) to color the map with the smallest number of colors.
Design
an algorithm for the following problem: Given a set of n points in the
Cartesian plane, determine whether all of them lie on the same circumference.
Write
a program that reads as its inputs the (x, y) coordinates of the endpoints of
two line segments P1Q1 and P2Q2 and determines whether the segments have a
common point.
Related Topics