Theory and Practice of Precipitation Gravimetry: Solubility Considerations

Theory and Practice

A precipitation gravimetric analysis must have several important attributes. First, the precipitate must be of low solubility, high purity, and of known composition if its mass is to accurately reflect the analyte’s mass. Second, the precipitate must be in a form that is easy to separate from the reaction mixture. The theoretical and exper- imental details of precipitation gravimetry are reviewed in this section.

Solubility Considerations 

An accurate precipitation gravimetric method requires that the precipitate’s solubility be minimal. Many total analysis techniques can rou- tinely be performed with an accuracy of better than ±0.1%. To obtain this level of accuracy, the isolated precipitate must account for at least 99.9% of the analyte. By extending this requirement to 99.99% we ensure that accuracy is not limited by the precipitate’s solubility.

Solubility losses are minimized by carefully controlling the composition of the solution in which the precipitate forms. This, in turn, requires an understanding of the relevant equilibrium reactions affecting the precipitate’s solubility. For example, Ag+ can be determined gravimetrically by adding Cl– as a precipitant, forming a precipitate of AgCl.

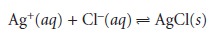                       8.1

If this is the only reaction considered, we would falsely conclude that the precipi- tate’s solubility, S_AgCl, is given by

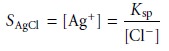                               8.2

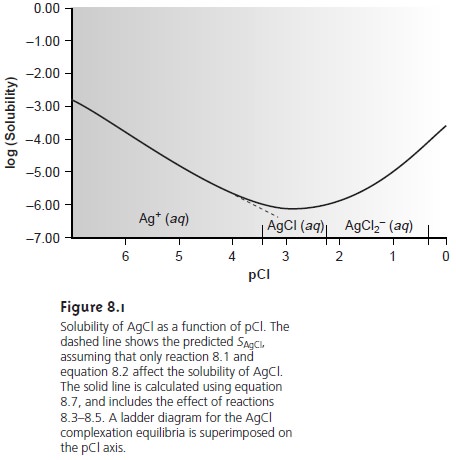
and that solubility losses may be minimized by adding a large excess of Cl–. In fact, as shown in Figure 8.1, adding a large excess of Cl– eventually increases the precipi- tate’s solubility.

To understand why AgCl shows a more complex solubility relationship than that suggested by equation 8.2, we must recognize that Ag+ also forms a series of soluble chloro-complexes

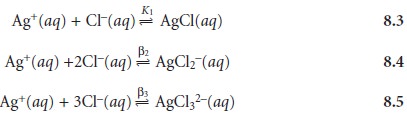
The solubility of AgCl, therefore, is the sum of the equilibrium concentrations for all soluble forms of Ag+.

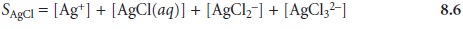
Substituting the equilibrium constant expressions for reactions 8.3–8.5 into equation 8.6 defines the solubility of AgCl in terms of the equilibrium concentration of Cl–

Equation 8.7 explains the solubility curve for AgCl shown in Figure 8.1. As Cl– is added to a solution of Ag+, the solubility of AgCl initially decreases because of re- action 8.1. Note that under these conditions, the final three terms in equation 8.7 are small, and that equation 8.1 is sufficient to describe the solubility of AgCl. In- creasing the concentration of chloride, however, leads to an increase in the solubil- ity of AgCl due to the soluble chloro-complexes formed in reactions 8.3–8.5.*

Clearly the equilibrium concentration of chloride is an important parameter if the concentration of silver is to be determined gravimetrically by precipitating AgCl. In particular, a large excess of chloride must be avoided.

Another important parameter that may affect a precipitate’s solubility is the pH of the solution in which the precipitate forms. For example, hydroxide precipitates, such as Fe(OH)₃, are more soluble at lower pH levels at which the concentration of OH– is small. The effect of pH on solubility is not limited to hydroxide precipitates, but also affects precipitates containing basic or acidic ions. The solubility of Ca₃(PO₄)₂ is pH-dependent because phosphate is a weak base. The following four reactions, therefore, govern the solubility of Ca₃(PO₄)₂.

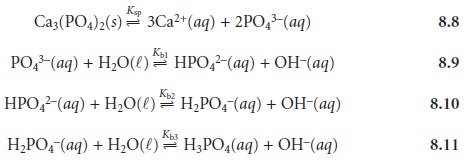
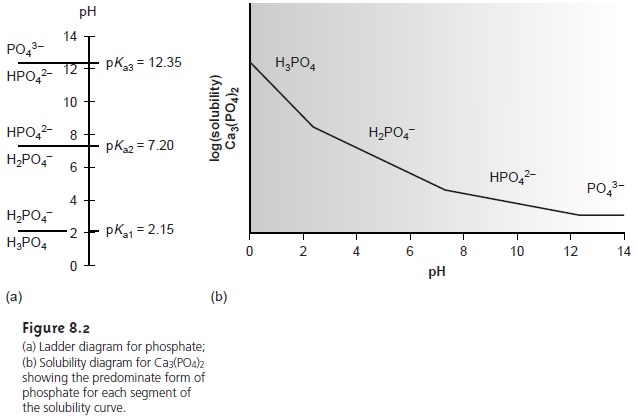
Depending on the solution’s pH, the predominate phosphate species is either PO₄3–, HPO₄2–, H₂PO₄–, or H₃PO₄. The ladder diagram for phosphate, shown in Figure 8.2a, provides a convenient way to evaluate the pH-dependent solubility of phos- phate precipitates. When the pH is greater than 12.4, the predominate phosphate species is PO₄3–, and the solubility of Ca₃(PO₄)₂ will be at its minimum because only reaction 8.8 occurs to an appreciable extent (see Figure 8.2b). As the solution becomes more acidic, the solubility of Ca₃(PO₄)₂ increases due to the contributions of reactions 8.9–8.11.

Solubility can often be decreased by using a nonaqueous solvent. A precip- itate’s solubility is generally greater in aqueous solutions because of the ability of water molecules to stabilize ions through solvation. The poorer solvating ability of nonaqueous solvents, even those that are polar, leads to a smaller solu- bility product. For example, PbSO₄ has a K_sp of 1.6 x 10–8 in H₂O, whereas in a 50:50 mixture of H₂O/ethanol the K_sp at 2.6 x 10–12 is four orders of magnitude smaller.