Precipitation Gravimetry: Evaluating Precipitation Gravimetry

Evaluating Precipitation Gravimetry

Scale of Operation 

The scale of operation for precipitation gravimetry is governed by the sensitivity of the balance and the availability of sample. To achieve an accu- racy of ±0.1% using an analytical balance with a sensitivity of ±0.1 mg, the precipi- tate must weigh at least 100 mg. As a consequence, precipitation gravimetry is usu- ally limited to major or minor analytes, and macro or meso samples. The analysis of trace level analytes or micro samples usually requires a microanalytical balance.

Accuracy 

For macro–major samples, relative errors of 0.1–0.2% are routinely achieved. The principal limitations are solubility losses, impurities in the precipitate, and the loss of precipitate during handling. When it is difficult to obtain a precipitate free from impurities, an empirical relationship between the precipitate’s mass and the mass of the analyte can be determined by an appropriate standardization.

Precision 

The relative precision of precipitation gravimetry depends on the amount of sample and precipitate involved. For smaller amounts of sample or precipitate, relative precisions of 1–2 ppt are routinely obtained. When working with larger amounts of sample or precipitate, the relative precision can be ex- tended to several parts per million. Few quantitative techniques can achieve this level of precision.

Sensitivity 

For any precipitation gravimetric method, we can write the following general equation relating the signal (grams of precipitate) to the absolute amount of analyte in the sample

Grams precipitate = k x grams of analyte             8.13

where k, the method’s sensitivity, is determined by the stoichiometry between the precipitate and the analyte. Note that equation 8.13 assumes that a blank has been used to correct the signal for the reagent’s contribution to the precipitate’s mass.

Consider, for example, the determination of Fe as Fe₂O₃. Using a conservation of mass for Fe we write

2 x moles Fe₂O₃ = moles Fe

Converting moles to grams and rearranging yields an equation in the form of 8.13

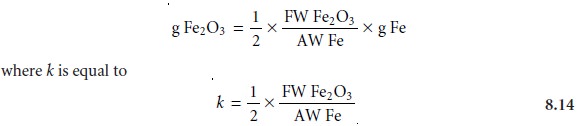
As can be seen from equation 8.14, we may improve a method’s sensitivity in two ways. The most obvious way is to increase the ratio of the precipitate’s molar mass to that of the analyte. In other words, it is desirable to form a precipitate with as large a formula weight as possible. A less obvious way to improve the calibration sensitivity is indicated by the term of 1/2 in equation 8.14, which accounts for the stoichiometry between the analyte and precipitate. Sensitivity also may be improved by forming precipitates containing fewer units of the analyte.

Selectivity 

Due to the chemical nature of the precipitation process, precipitants are usually not selective for a single analyte. For example, silver is not a selective precipitant for chloride because it also forms precipitates with bromide and iodide. Consequently, interferents are often a serious problem that must be considered if accurate results are to be obtained.

Time, Cost, and Equipment 

Precipitation gravimetric procedures are time-intensive and rarely practical when analyzing a large number of samples. However, since much of the time invested in precipitation gravimetry does not require an analyst’s immedi- ate supervision, it may be a practical alternative when working with only a few sam- ples. Equipment needs are few (beakers, filtering devices, ovens or burners, and bal- ances), inexpensive, routinely available in most laboratories, and easy to maintain.