Student Activity Questions and Answers

Solution:

Progress Check

Say True or False

1. Every chord of a circle contains exactly two points of the circle.

2. All radii of a circle are of same length.

3. Every radius of a circle is a chord.

4. Every chord of a circle is a diameter.

5. Every diameter of a circle is a chord.

6. There can be any number of diameters for a circle.

7. Two diameters cannot have the same end-point.

8. A circle divides the plane into three disjoint parts.

9. A circle can be partitioned into a major arc and a minor arc.

10. The distance from the centre of a circle to the circumference is that of a diameter

Thinking Corner

1. How many sides does a circle have ?

2. Is circle, a polygon?

Progress Check

1. The radius of the circle is 25 cm and the length of one of its chord is 40cm. Find the distance of the chord from the centre.

2. Draw three circles passing through the points P and Q, where PQ = 4cm.

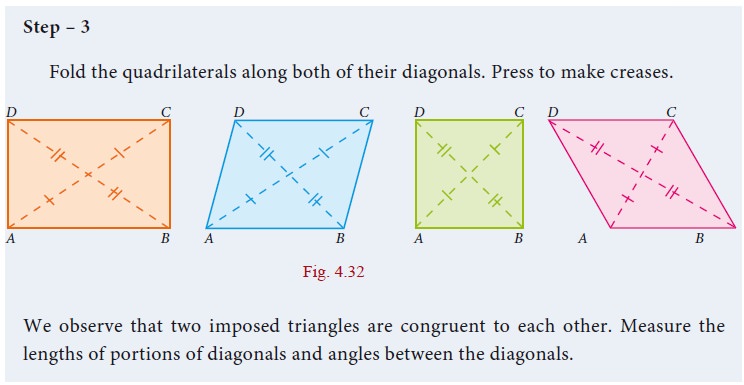
Activity − 5

Procedure

1. Draw a circle with centre O and with suitable radius.

2. Make it a semi-circle through folding. Consider the point A, B on it.

3. Make crease along AB in the semi circles and open it.

4. We get one more crease line on the another part of semi circle, name it as CD (observe AB = CD)

5. Join the radius to get the ΔOAB and ΔOCD .

6. Using trace paper, take the replicas of triangle ΔOAB and ΔOCD.

7. Place these triangles ΔOAB and ΔOCD one on the other.

Observation

1. What do you observe? Is ΔOAB ≡ ΔOCD ? Answer: Yes ΔOAB ≡ ΔOCD 

2. Construct perpendicular line to the chords AB and CD passing through the centre O. Measure the distance from O to the chords.

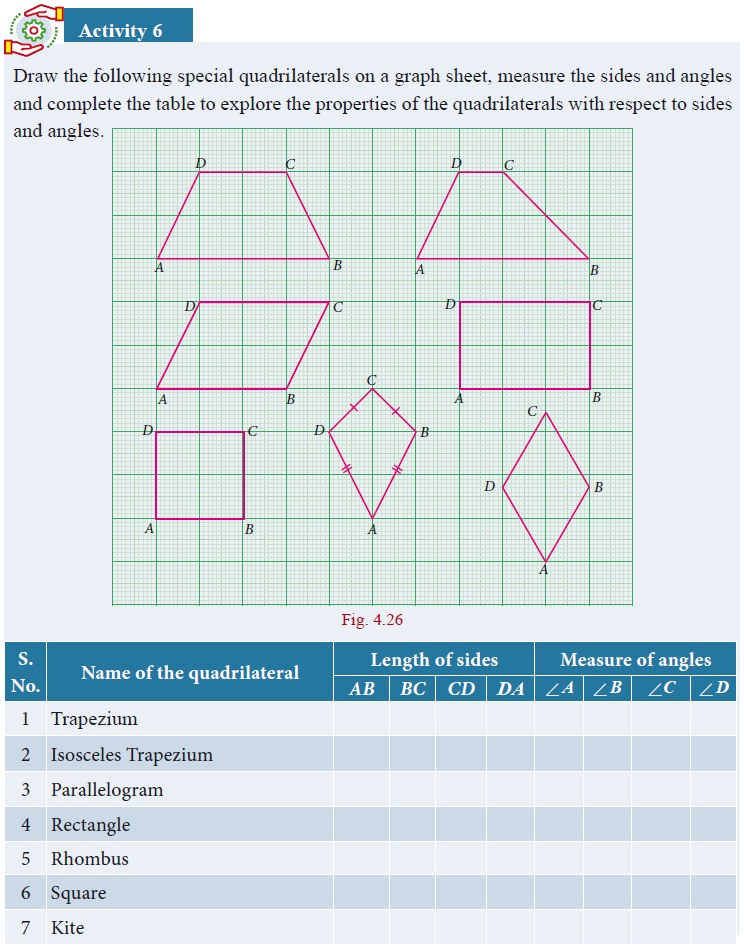
Activity – 6

Procedure :

1. Draw three circles of any radius with centre O on a chart paper.

2. From these circles, cut a semi-circle, a minor segment and a major segment.

3. Consider three points on these segment and name them as A, B and C.

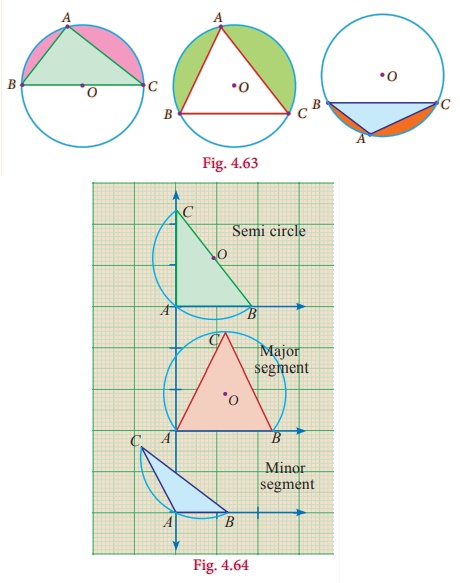
4. (iv) Cut the triangles and paste it on the graph sheet so that the point A coincides with the origin as shown in the figure.

Observation :

(i) Angle in a Semi-Circle is right angle.

(ii) Angle in a major segment is acute angle.

(iii) Angle in a minor segment is obtuse angle.

Progress Check

i. Draw the outline of different size of bangles and try to find out the centre of each using set square.

ii. Trace the given cresent and complete as full moon using ruler and compass.

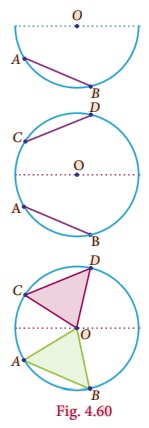
Activity − 7

Procedure

1. Draw a circle of any radius with centre O.

2. Mark any four points A, B, C and D on the boundary. Make a cyclic quadrilateral ABCD and name the angles as in Fig. 4.78

3. Make a replica of the cyclic quadrilateral ABCD with the help of  tracing paper.

4. Make the cutout of the angles A, B, C and D as in Fig. 4.79

5. Paste the angle cutout ∠1, ∠2, ∠3 and ∠4 adjacent to the angles  opposite to A, B, C and D as in Fig. 4.80

6. Measure the angles ∠1 + ∠3, and ∠2 + ∠4.

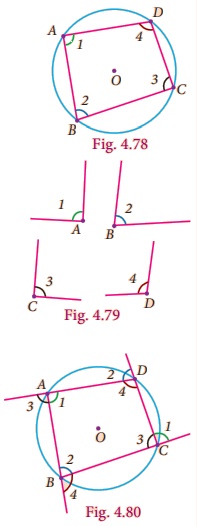
Observe and complete the following:

1. (i) ∠A + ∠C = 180°

(ii) ∠B + ∠D = 180°

(iii) ∠C + ∠A = 180°

(iv) ∠D +∠B = 180°

2. Sum of opposite angles of a cyclic quadrilateral is 180°.

3. The opposite angles of a cyclic quadrilateral is _______.

Progress Check

1. If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is _____________.

2. As the length of the chord decreases, the distance from the centre _____________.

3. If one side of a cyclic quadrilateral is produced then the exterior angle is _____________ to the interior opposite angle.

4. Opposite angles of a cyclic quadrilateral are _____________.