Cyclic Quadrilaterals

Cyclic Quadrilaterals

Now, let us see a special quadrilateral with its properties called “Cyclic Quadrilateral”. A quadrilateral is called cyclic quadrilateral if all its four vertices lie on the circumference of the circle. Now we are going to learn the special property of cyclic quadrilateral.

Consider the quadrilateral ABCD whose vertices lie on a circle. We want to show that its opposite angles are supplementary. Connect the centre O of the circle with each vertex. You now see four radii OA, OB, OC and OD giving rise to four isosceles triangles OAB, OBC, OCD and ODA. The sum of the angles around the centre of the circle is 360° . The angle sum of each isosceles triangle is 180°

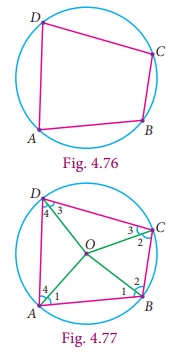
Thus, we get from the figure,

2×( ∠ 1+ ∠ 2+ ∠ 3+ ∠ 4) + Angle at centre O = 4× 180°

2×(∠ 1+∠ 2+∠ 3+∠ 4) + 360° = 720°

Simplifying this,

( ∠ 1+ ∠ 2+ ∠ 3+ ∠ 4) = 180°.

You now interpret this as

(i) (∠ 1+∠ 2) + (∠ 3+∠ 4) = 180° (Sum of opposite angles B and D)

(ii) ( ∠ 1+ ∠ 4) + ( ∠ 2+ ∠ 3) = 180° (Sum of opposite angles A and C)

Now the result is given as follows.

Theorem 12 Opposite angles of a cyclic quadrilateral are supplementary.

Let us see the converse of theorem 12, which is very useful in solving problems

Converse of Theorem 12 If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic.

Activity − 7

Procedure

1. Draw a circle of any radius with centre O.

2. Mark any four points A, B, C and D on the boundary. Make a cyclic quadrilateral ABCD and name the angles as in Fig. 4.78

3. Make a replica of the cyclic quadrilateral ABCD with the help of  tracing paper.

4. Make the cutout of the angles A, B, C and D as in Fig. 4.79

5. Paste the angle cutout ∠1, ∠2, ∠3 and ∠4 adjacent to the angles  opposite to A, B, C and D as in Fig. 4.80

6. Measure the angles ∠1 + ∠3, and ∠2 + ∠4.

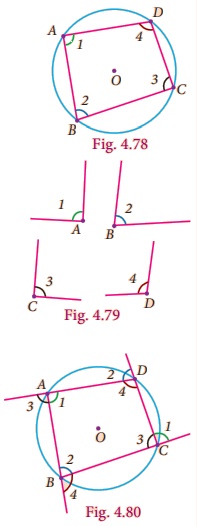
Observe and complete the following:

1. (i) ∠A + ∠C = 180°

(ii) ∠B + ∠D = 180°

(iii) ∠C + ∠A = 180°

(iv) ∠D +∠B = 180°

2. Sum of opposite angles of a cyclic quadrilateral is 180°.

3. The opposite angles of a cyclic quadrilateral is _______.

Example 4.10

If PQRS is a cyclic quadrilateral in which ∠PSR = 70° and ∠QPR = 40°, then find ∠PRQ (see Fig. 4.81).

Solution

PQRS is a cyclic quadrilateral

Given ∠ PSR = 70°

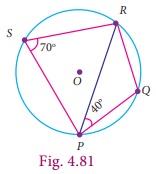
∠PSR + ∠PQR = 180° (state reason________)

70° + ∠PQR = 180°

∠PQR = 180° − 70°

∠PQR = 110°

In ΔPQR we have,

∠PQR + ∠PRQ + ∠QPR = 180° (state reason_________)

110° + ∠PRQ + 40° = 180°

∠PRQ = 180° − 150°

∠PRQ = 30°

Exterior Angle of a Cyclic Quadrilateral

An exterior angle of a quadrilateral is an angle in its exterior formed by one of its sides and the extension of an adjacent side.

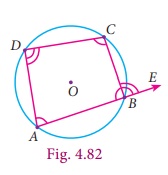
Let the side AB of the cyclic quadrilateral ABCD be extended to E. Here ∠ABC and ∠CBE are linear pair, their sum is 180° and the angles ∠ABC and ∠ADC are the opposite angles of a cyclic quadrilateral, and their sum is also 180°. From this, ∠ABC + CBE = ∠ABC + ADC and finally we get ∠CBE = ∠ADC . Similarly it can be proved for other angles.

Theorem 13 If one side of a cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.

Progress Check

1. If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is _____________.

2. As the length of the chord decreases, the distance from the centre _____________.

3. If one side of a cyclic quadrilateral is produced then the exterior angle is _____________ to the interior opposite angle.

4. Opposite angles of a cyclic quadrilateral are _____________.

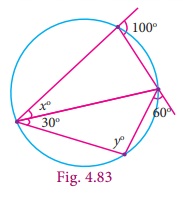
Example 4.11

In the figure given, find the value of x° and y° .

Solution

By the exterior angle property of a cyclic quadrilateral,

we get, y°=100° and

x° + 30° = 60° and so x° = 30°