Construction of the Circumcentre of a Triangle

Construction of the Circumcentre of a Triangle

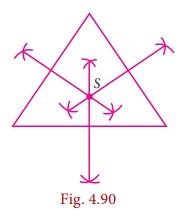
Circumcentre

The Circumcentre is the point of concurrency of the Perpendicular bisectors of the sides of a triangle.

It is usually denoted by S.

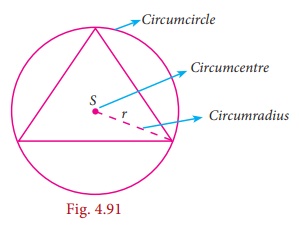
Circumcircle

The circle passing through all the three vertices of the triangle with circumcentre (S) as centre is called circumcircle.

Circumradius

The line segment from any vertex of a triangle to the Circumcentre of a given triangle is called circumradius of the circumcircle.

Activity 11

Objective: To construct a perpendicular bisector of a line segment using paper folding.

Procedure: Make a line segment on a paper by folding it and name it as PQ. Fold PQ in such a way that P falls on Q and thereby creating a crease RS. This line RS is the perpendicular bisector of PQ.

Activity 12

Objective: To locate the circumcentre of a triangle using paper folding.

Procedure: Using Activity 12, find the perpendicular bisectors for any two sides of the given triangle. The meeting point of these is the circumcentre of the given triangle.

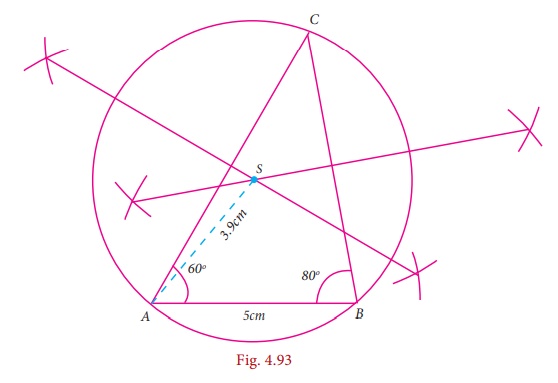
Example 4.14

Construct the circumcentre of the ΔABC with AB = 5 cm, ∠A = 60º and ∠ B = 80º. Also draw the circumcircle and find the circumradius of the ΔABC.

Solution

Step 1

Draw the ΔABC with the given measurements

Step 2

Construct the perpendicular bisector of any two sides (AC and BC) and let them meet at S which is the circumcentre.

Step 3

S as centre and SA = SB = SC as radius, draw the Circumcircle to passes through A,B and C.

Circumradius = 3.9 cm.

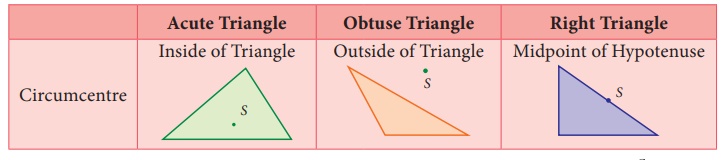
Note

Where do the Circumcentre lie in the given triangles.