Exercise 4.2: Quadrilaterals

Exercise 4.2

1. The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.

2. In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x–10 and x + 4. Find the value of x and the measure of all the ∠angles.

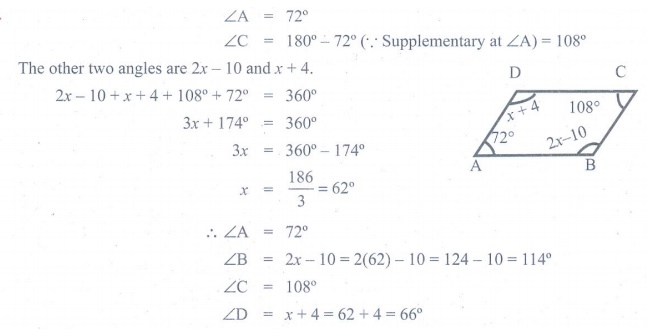
3. ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB =46°, find ∠OBC

4. The lengths of the diagonals of a Rhombus are 12 cm and 16 cm . Find the side of the rhombus.

5. Show that the bisectors of angles of a parallelogram form a rectangle .

6. If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram.

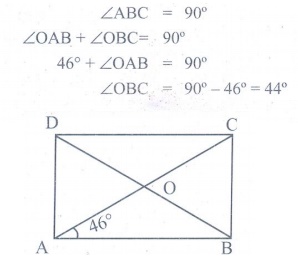
7. Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b , c || d , e || f , find the marked angles between

(i) b and c

(ii) d and e

(iii) d and f

(iv) c and f

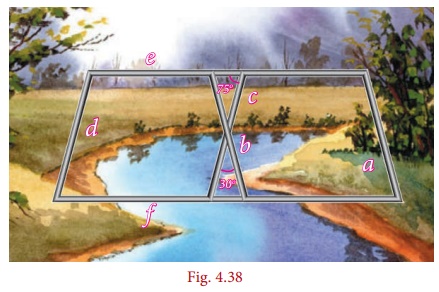
8. In the given Fig. 4.39, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°

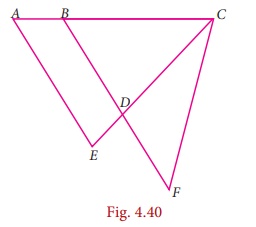
9. In the given Fig. 4.40, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles).

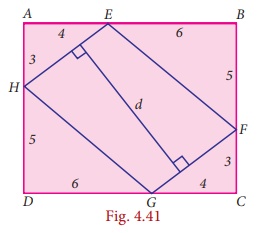
10. In the Fig. 4.41 , ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to  and  ?

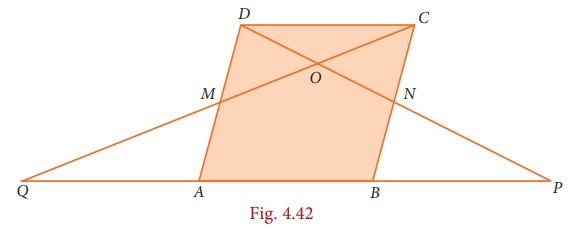
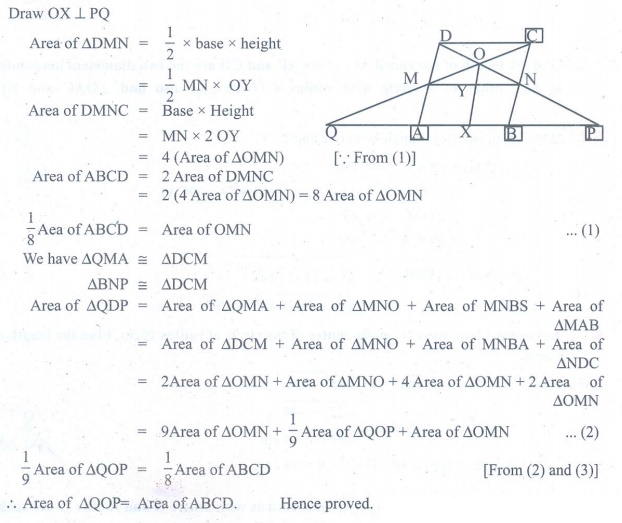
11. In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is 9/8 of the area of the parallelogram ABCD.