Special Names, Types, Properties, Theorem with proof, Example Solved Problems | Geometry | Maths - Quadrilaterals | 9th Maths : UNIT 4 : Geometry
Chapter: 9th Maths : UNIT 4 : Geometry
Quadrilaterals
Quadrilaterals
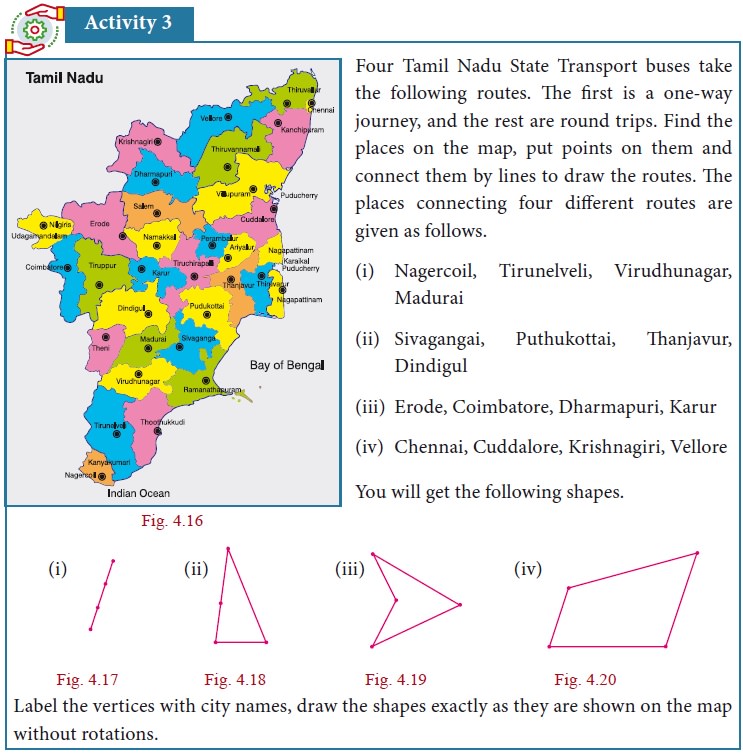
We observe that the first is a single line, the four points are collinear. The other three are closed shapes made of straight lines, of the kind we have seen before. We need names to call such closed shapes, we will call them polygons from now on.
How do polygons look? They have sides, with points at either end. We call these points vertices of the polygon. The sides are line segments joining the vertices. The word poly stands for many, and a polygon is a many-sided figure.

How many sides can a polygon have? One? But that is just a line segment. Two ? But how can you get a closed shape with two sides? Three? Yes, and this is what we know as a triangle. Four sides?
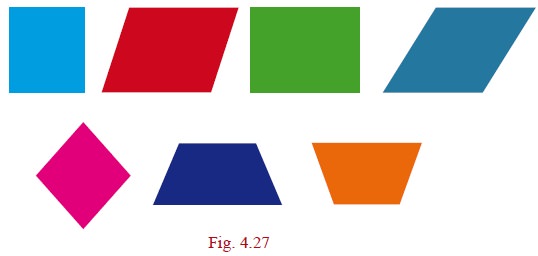
Squares and rectangles are examples of polygons with 4 sides but they are not the only ones. Here are some examples of 4-sided polygons. We call them quadrilaterals.

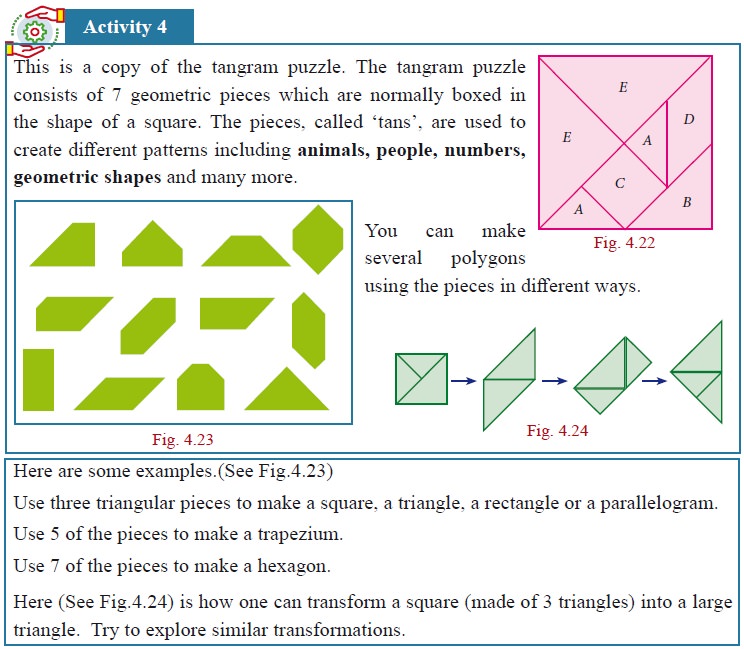
Solution:


Do you see some patterns in all the data you have recorded? We see many interesting properties, but how do we know whether these are true in general, or happen to hold only for these figures? It is not even clear what properties we should look for. The best way to answer this is to go back to what we already know and look at it from this viewpoint. We know rectangles, so we can ask what properties rectangles have. Here they are:
o Opposite sides are equal. (1)
o All angles are equal, each is 90 degrees. (2)
o Adjacent sides may or may not be equal. (3)
Among these, the last statement really says nothing! (Mathematicians call such statements trivial, and they prefer not to write them down.) Note that adjacent sides have a vertex in common, and opposite sides have no vertex in common. A square has all these properties but the third is replaced by; Adjacent sides are equal. (4) Now we can combine (1) and (4) and say that in a square, all sides are equal.
Thus we see that every square is a rectangle but a rectangle need not be a square. This suggests a way of classifying quadrilaterals, of grouping them according to whether some sides are equal or not, some angles are equal or not.
1. Special Names for Some Quadrilaterals
1. A parallelogram is a quadrilateral in which opposite sides are parallel and equal.
2. A rhombus is a quadrilateral in which opposite sides are parallel and all sides are equal.
3. A trapezium is a quadrilateral in which one pair of opposite sides are parallel.
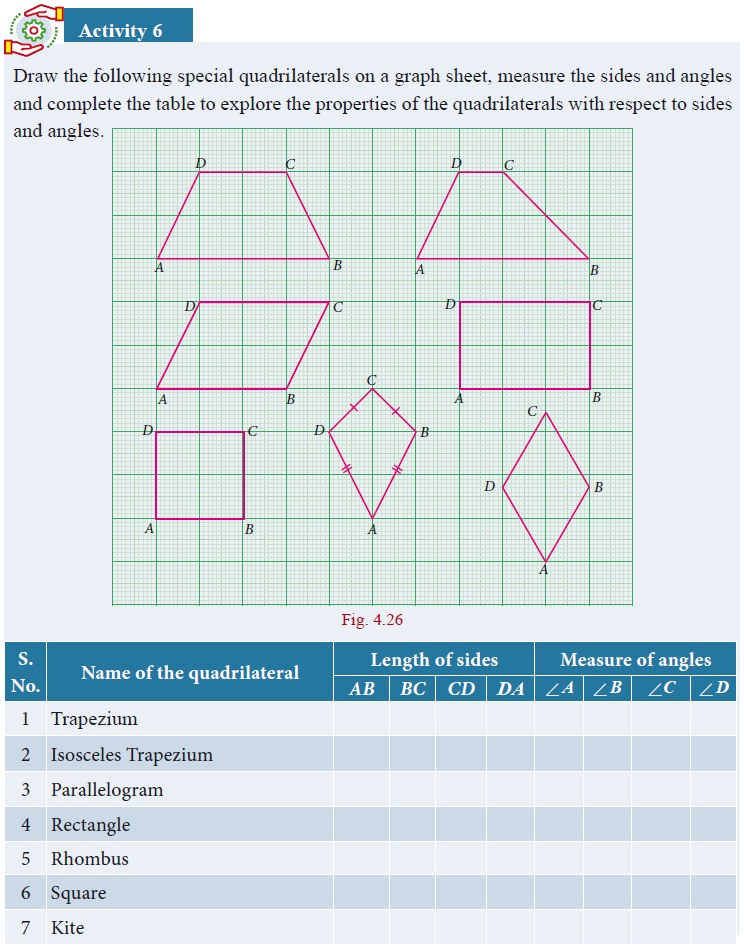
Draw a few parallellograms, a few rhombuses (correctly called rhombii, like cactus and cactii) and a few trapeziums (correctly written trapezia).
The great advantage of listing properties is that we can see the relationships among them immediately.
o Every parallelogram is a trapezium, but not necessarily the other way.
o Every rhombus is a parallelogram, but not necessarily the other way.
o Every rectangle is a parallelogram, but not necessarily the other way.
o Every square is a rhombus and hence every square is a parallelogram as well.
For “not necessarily the other way” mathematicians usually say “the converse is not true”. A smart question then is: just when is the other way also true? For instance, when is a parallelogram also a rectangle? Any parallelogram in which all angles are also equal is a rectangle. (Do you see why?) Now we can observe many more interesting properties. For instance, we see that a rhombus is a parallelogram in which all sides are also equal.
2. More Special Names
When all sides of a quadrilateral are equal, we call it equilateral. When all angles of a quadrilateral are equal, we call it equiangular . In triangles, we talked of equilateral triangles as those with all sides equal. Now we can call them equiangular triangles as well!
We thus have:
A rhombus is an equilateral parallelogram.
A rectangle is an equiangular parallelogram.
A square is an equilateral and equiangular parallelogram.
Here are two more special quadrilaterals, called kite and isosceles trapezium.
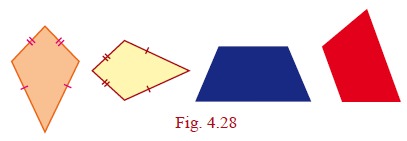
3. Types of Quadrilaterals


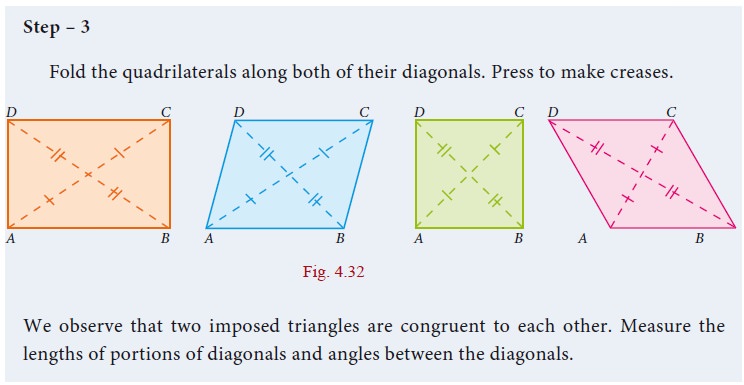
Also do the same for the quadrilaterals such as Trapezium, Isosceles Trapezium and Kite.
From the above activity, measure the lengths of diagonals and angles between the diagonals and record them in the table below:
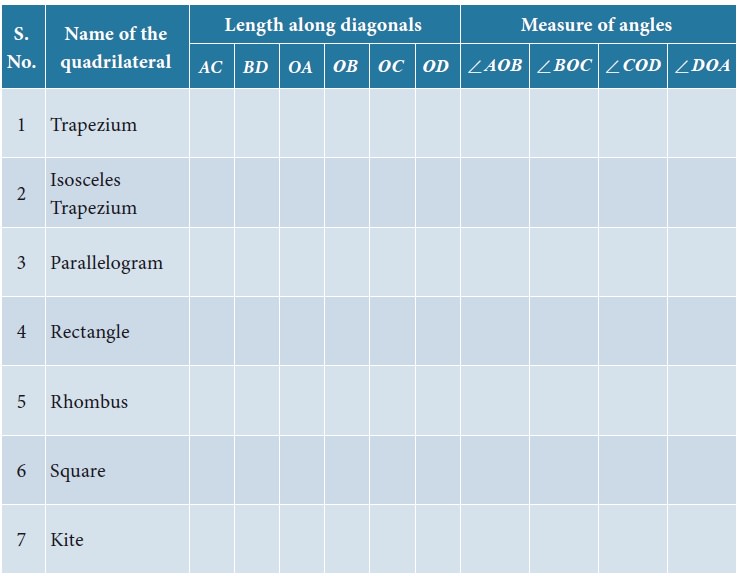
4. Properties of Quadrilaterals
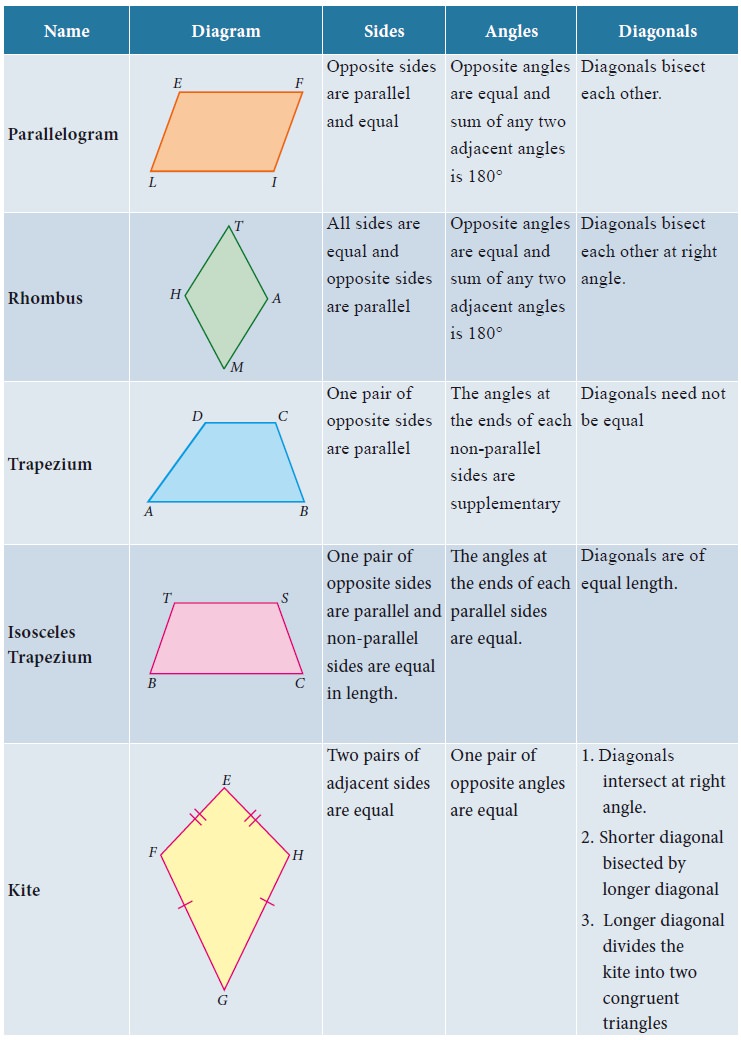


5. Properties of Parallelogram
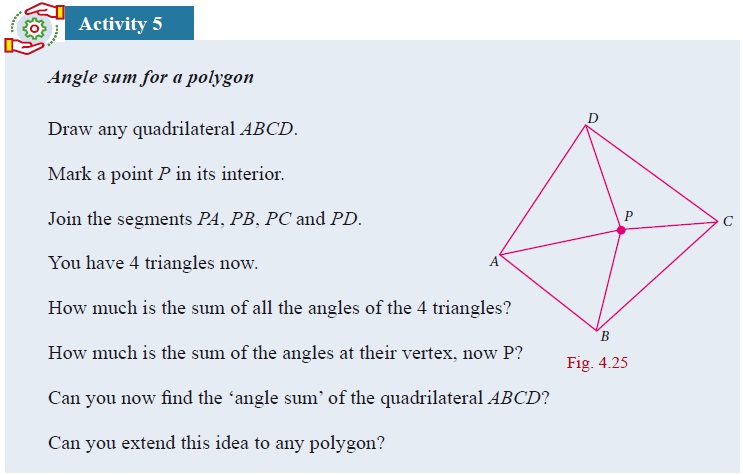
We can now embark on an interesting journey. We can tour among lots of quadrilaterals, noting down interesting properties. What properties do we look for, and how do we know they are true?
For instance, opposite sides of a parallelogram are parallel, but are they also equal? We could draw any number of parallelograms and verify whether this is true or not. In fact, we see that opposite sides are equal in all of them. Can we then conclude that opposite sides are equal in all parallelograms? No, because we might later find a parallelogram, one which we had not thought of until then, in which opposite sides are unequal. So, we need an argument, a proof.
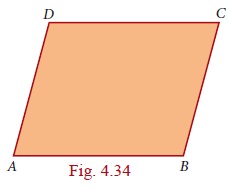
Consider the parallelogram ABCD in the given Fig. 4.34. We believe that AB = CD and AD = BC, but how can we be sure? We know triangles and their properties. So we can try and see if we can use that knowledge. But we don’t have any triangles in the parallelogram ABCD.
This is easily taken care of by joining AC. (We could equally well have joined BD, but let it be AC for now.) We now have 2 triangles ADC and ABC with a common side AC. If we could somehow prove that these two triangles are congruent, we would get AB = CD and AD = BC, which is what we want!
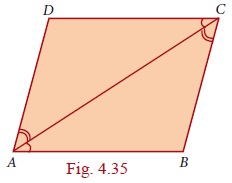
Is there any hope of proving that DADC and DABC are congruent? There are many criteria for congruence, it is not clear which one is relevant here.
So far we have not used the fact that ABCD is a parallelogram at all. So we need to use the facts that AB|| DC and AD|| BC to show that DADC and DABC are congruent. From sides being parallel we have to get to some angles being equal. Do we know any such properties? Yes we do, and that is all about transversals!
Now we can see it clearly. AD||BC and AC is a transversal, hence ∠DAC = BCA. Similarly, AB|| DC, AC is a transversal, hence ∠BAC = ∠DCA. With AC as common side, the ASA criterion tells us that ∆ADC and ∆ABC are congruent, just what we needed. From this we can conclude that AB = CD and AD = BC.
Thus opposite sides are indeed equal in a parallelogram.
The argument we now constructed is written down as a formal proof in the following manner.
Theorem 1
In a parallelogram, opposite sides are equal
Given ABCD is a parallelogram
To Prove AB=CD and DA=BC
Construction Join AC
Proof
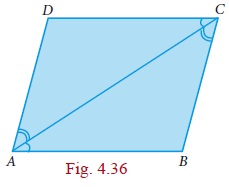
Since ABCD is a parallelogram
AD||BC and AC is the transversal
∠DAC = ∠BCA →(1) (alternate angles are equal)
AB||DC and AC is the transversal
∠BAC = ∠DCA →(2) (alternate angles are equal)
In ΔADC and ΔCBA
∠DAC = ∠BCA from (1)
AC is common
∠DCA = ∠BAC from (2)
ΔADC ≈ ΔCBA (By ASA)
Hence AD = CB and DC = BA (Corresponding sides are equal)
Along the way in the proof above, we have proved another property that is worth recording as a theorem.
Theorem 2
A diagonal of a parallelogram divides it into two congruent triangles.
Notice that the proof above established that ∠DAC = ∠BCA and ∠BAC = ∠DCA.
Hence we also have, in the figure above,
∠BCA + ∠BAC = ∠DCA + ∠DAC
But we know that:
∠B + ∠BCA + ∠BAC = 180
and ∠D + ∠DCA + ∠DAC = 180
Therefore we must have that ∠B = ∠D. Fig. 4.37
With a little bit of work, proceeding similarly, we could have shown that ∠A = ∠C as well.
Thus we have managed to prove the following theorem:
Theorem 3
The opposite angles of a parallelogram are equal.
Now that we see congruence of triangles as a good “strategy”, we can look for more triangles. Consider both diagonals AC and DB. We already know that DADC and DCBA are congruent. By a similar argument we can show that DDAB and DBCD are congruent as well. Are there more congruent triangles to be found in this figure ?
Yes. The two diagonals intersect at point O. We now see 4 new DAOB, DBOC, DCOD and DDOA. Can you see any congruent pairs among them?
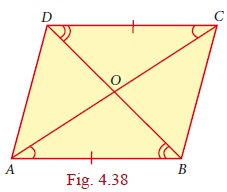
Since AB and CD are parallel and equal, one good guess is that ΔAOB and ΔCOD are congruent. We could again try the ASA crierion, in which case we want ∠OAB = ∠OCD and ∠ABO = ∠CDO. But the first of these follows from the fact that ∠CAB = ∠ACD (which we already established) and observing that ∠CAB and ∠OAB are the same (and so also ∠OCD and ∠ACD). We now use the fact that BD is a transversal to get that ∠ABD = ∠CDB, but then ∠ABD is the same as ∠ABO, ∠CDB is the same as ∠CDO, and we are done.
Again, we need to write down the formal proof, and we have another theorem.
Theorem 4
The diagonals of a parallelogram bisect each other.
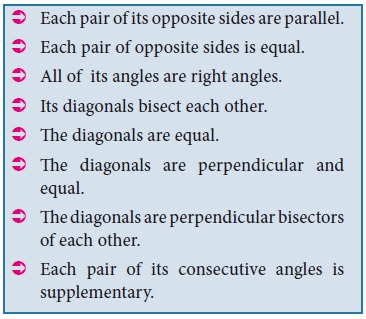
It is time now to reinforce our concepts on parallelograms. Consider each of the given statements, in the adjacent box, one by one. For each statement, we can conclude that it is a quadrilateral. If the quadrilateral happens to be a parallelogram, what type of parallelogram is it?
Now we begin with lots of interesting properties of parallelograms. Can we try and prove some property relating to two or more parallelograms ? A simple case to try is when two parallelograms share the same base, as in Fig.4.39
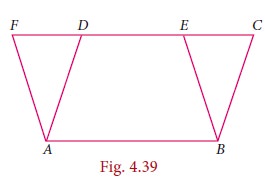
We see parallelograms ABCD and ABEF are on the common base AB. At once we can see a pair of triangles for being congruent DADF and DBCE. We already have that AD = BC and AF = BE. But then since AD|| BC and AF|| BE, the angle formed by AD and AF must be the same as the angle formed by BC tand BE. Therefore ∠DAF = ∠CBE. Thus DADF and DBCE are congruent.
That is an interesting observation; can we infer anything more from this ? Yes, we know that congruent triangles have the same area. This makes us think about the areas of the parallelograms ABCD and ABEF.
Area of ABCD = area of quadrilateral ABED + area of DBCE
= area of quadrilateral ABED + area of DADF
= area of ABEF
Thus we have proved another interesting theorem:
Theorem 5:
Parallelograms on the same base and between the same parallels are equal in area.
In this process, we have also proved other interesting statements. These are called Corollaries, which do not need separate detailed proofs.
Corollary 1: Triangles on the same base and between the same parallels are equal in area.
Corollary 2: A rectangle and a parallelogram on the same base and between the same parallels are equal in area.
These statements that we called Theorems and Corollaries, hold for all parallelograms, however large or small, with whatever be the lengths of sides and angles at vertices.
Example 4.1
In a parallelogram ABCD, the bisectors of the consecutive angles ∠A and ∠B insersect at P. Show that ∠APB = 90°
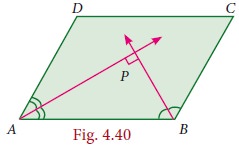
Solution
ABCD is a parallelogram AP and BP are bisectors of consecutive angles ∠A and ∠B.
Since the consecutive angles of a parallelogram are supplementary
∠A + ∠B = 180°
½ ∠A + ½ ∠B = 180°/2
so ∠PAB + ∠PBA = 90°
In ΔAPB,
∠PAB + ∠APB + ∠PBA = 180° (angle sum property of triangle)
∠APB = 180° – [∠PAB + ∠PBA]
= 180° – 90° = 90°
Hence Proved.
Example 4.2
In the Fig.4.41 ABCD is a parallelogram, P and Q are the mid-points of sides AB and DC respectively. Show that APCQ is a parallelogram.
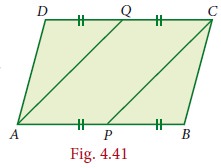
Solution
Since P and Q are the mid points of
AB and DC respectively

Also , AB || DC
AP || QC (3) [a ABCD is a parallelogram]
Thus , in quadrilateral APCQ we have AP= QC and AP || QC [from (2) and ( 3)]
Hence , quadrilateral APCQ is a parallelogram.
Example 4.3
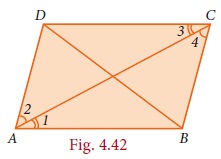
ABCD is a parallelogram Fig.4.42 such that ∠BAD = 120o and AC bisects ∠BAD show that ABCD is a rhombus.
Solution
Given ∠BAD = D C 120° and AC bisects ∠BAD
∠BAC = 1/2 x 120° = 60°
∠1 = ∠2 = 60°
AD || BC and AC is the traversal
∠2 = ∠4 = 60°
Δ ABC is isosceles triangle [∠1 = ∠4 = 60°]
AB = BC
Parallelogram ABCD is a rhombus.
Example 4.4
In a parallelogram ABCD , P and Q are the points on line DB such that PD = BQ show that APCQ is a parallelogram
Solution
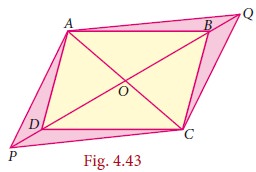
ABCD is a parallelogram.
OA = OC and
OB = OD (Diagonals bisect each other)
now OB + BQ = OD + DP
OQ = OP and OA = OC
APCQ is a parallelogram.
Related Topics