Construction of Orthocentre of a Triangle

Construction of Orthocentre of a Triangle

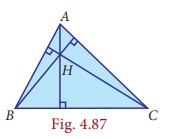
Orthocentre

The orthocentre is the point of concurrency of the altitudes of a triangle. Usually it is denoted by H.

Activity 9

Objective To construct a perpendicular to a line segment from an external point using paper folding.

Procedure Draw a line segment AB and mark an external point P. Move B along BA till the fold passes through P and crease it along that line. The crease thus formed is the perpendicular to AB through the external point P.

Activity 10

Objective To locate the Orthocentre of a triangle using paper folding.

Procedure Using the above Activity with any two vertices of the triangle as external points, construct the perpendiculars to opposite sides. The point of intersection of the perpendiculars is the Orthocentre of the given triangle.

Example 4.13

Construct ΔPQR whose sides are PQ = 6 cm ∠Q = 600 and QR = 7 cm and locate its Orthocentre.

Solution

Step 1 Draw the ΔPQR with the given measurements.

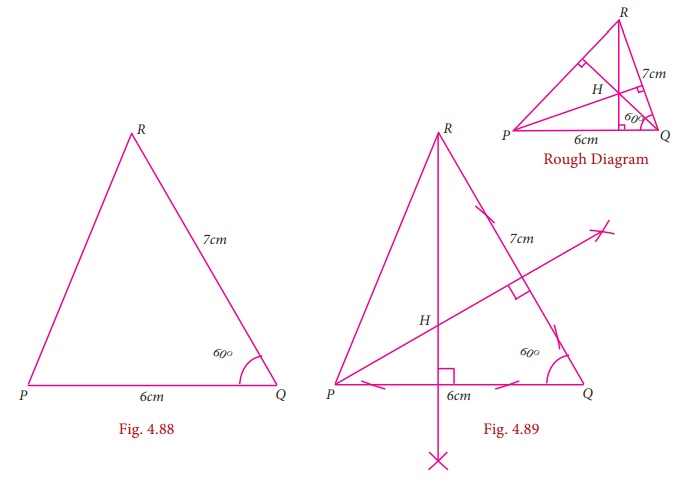
Step 2:

Construct altitudes from any two vertices (say) R and P, to their opposite sides PQ and QR respectively.

The point of intersection of the altitude H is the Orthocentre of the given ΔPQR.

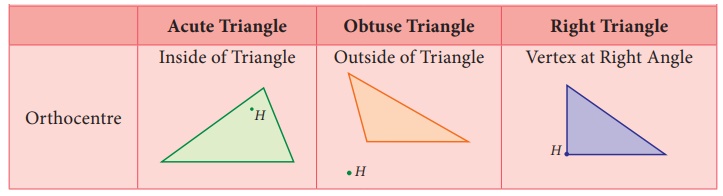
Note

Where do the Orthocentre lie in the given triangles.