Construction of the Centroid of a Triangle

Construction of the Centroid of a Triangle

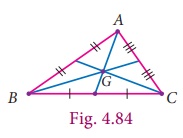
Centroid

The point of concurrency of the medians of a triangle is called the centroid of the triangle and is usually denoted by G.

Activity 8

Objective To find the mid-point of a line segment using paper folding

Procedure Make a line segment on a paper by folding it and name it PQ. Fold the line segment PQ in such a way that P falls on Q and mark the point of intersection of the line segment and the crease formed by folding the paper as M. M is the midpoint of PQ.

Example 4.12

Construct the centroid of ΔPQR whose sides are PQ = 8cm; QR = 6cm; RP = 7cm.

Solution

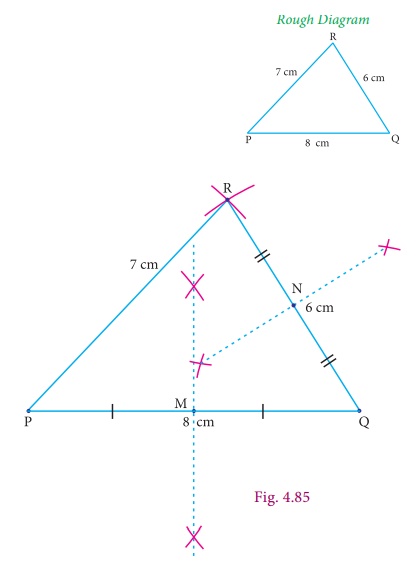
Step 1 : Draw ΔPQR using the given measurements PQ = 8cm QR = 6cm and RP = 7cm and construct the perpendicular bisector of any two sides (PQ and QR) to find the mid-points M and N of PQ and QR respectively.

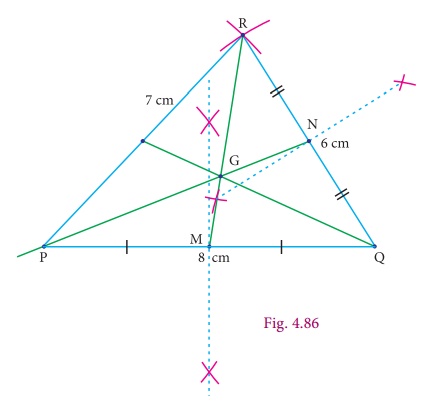
Step 2 : Draw the medians PN and RM and let them meet at G. The point G is the centroid of the given ΔPQR .

Note

• Three medians can be drawn in a triangle

• The centroid divides each median in the ratio 2:1 from the vertex.

• The centroid of any triangle always lie inside the triangle.

• Centroid is often described as the triangle’s centre of gravity (where the triangle balances evenly) and also as the barycentre.