Properties of Chords of a Circle

Properties of Chords of a Circle

In this chapter, already we come across lines, angles, triangles and quadrilaterals. Recently we have seen a new member circle. Using all the properties of these, we get some standard results one by one. Now, we are going to discuss some properties based on chords of the circle.

Considering a chord and a perpendicular line from the centre to a chord, we are going to see an interesting property.

1. Perpendicular from the Centre to a Chord

Consider a chord AB of the circle with centre O. Draw OC ⊥ AB and join the points OA, OB. Here, easily we get two triangles ΔAOC and ΔBOC (Fig.4.56).

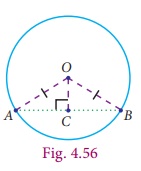
Can we prove these triangles are congruent? Now we try to prove this using the congruence of triangle rule which we have already learnt. ∠OCA = ∠OCB = 90° (OC ⊥ AB) and OA = OB is the radius of the circle. The side OC is common. RHS criterion tells us that ΔAOC and ΔBOC are congruent. From this we can conclude that AC = BC . This argument leads to the result as follows.

Theorem 7 The perpendicular from the centre of a circle to a chord bisects the chord.

Converse of Theorem 7 The line joining the centre of the circle and the midpoint of a chord is perpendicular to the chord.

Example 4.5

Find the length of a chord which is at a distance of 2√11 cm from the centre of a circle of radius 12cm.

Solution

Let AB be the chord and C be the mid point of AB

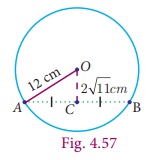
Therefore, OC ⊥ AB

Join OA and OC.

OA is the radius

Given OC = 2√11cm and OA = 12cm

In a right ΔOAC ,

using Pythagoras Theorem, we get,

AC 2 =OA2 −OC2

= 122 −(2√11)2

=144−44

= 100cm

AC2 = 100cm

AC = 10cm

Therefore, length of the chord AB = 2AC

= 2 × 10cm = 20cm

Note

Pythagoras theorem

One of the most important and well known results in  geometry is Pythagoras  Theorem. “In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides”.

In right Δ ABC, BC2 =AB2 +AC2 .

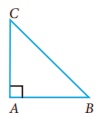
Application of this theorem is most useful in this unit.

Example 4.6

In the concentric circles, chord AB of the  outer circle cuts the inner circle at C and D as shown in the diagram. Prove that, AB − CD = 2AC

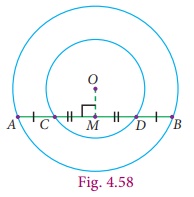
Solution

Given : Chord AB of the outer circle cuts the inner circle at C and D.

To prove

AB −CD = 2AC

Construction

Draw OM ⊥ AB

Proof

Since, OM ⊥ AB (By construction)

Also, OM ⊥ CD

Therefore, AM = MB ... (1) (Perpendicular drawn from centre to chord bisect it)

CM = MD ... (2)

Now, AB – CD = 2AM–2CM

= 2(AM–CM) from (1) and (2)

AB –CD =2AC

Progress Check

1. The radius of the circle is 25 cm and the length of one of its chord is 40cm. Find the distance of the chord from the centre.

2. Draw three circles passing through the points P and Q, where PQ = 4cm.

2. Angle Subtended by Chord at the Centre

Instead of a single chord we consider two equal chords. Now we are going to discuss another property.

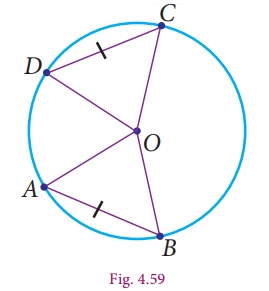
Let us consider two equal chords in the circle with centre O. Join the end points of the chords with the centre to get the triangles ΔAOB and ΔOCD , chord AB = chord CD (because the given chords are equal). The other sides are radii, therefore OA=OC and OB=OD. By SSS rule, the triangles are congruent, that is ΔOAB ≡ OCD . This gives m ∠AOB = m ∠COD. Now this leads to the following result.

Theorem 8 Equal chords of a circle subtend equal angles at the centre.

Activity − 5

Procedure

1. Draw a circle with centre O and with suitable radius.

2. Make it a semi-circle through folding. Consider the point A, B on it.

3. Make crease along AB in the semi circles and open it.

4. We get one more crease line on the another part of semi circle, name it as CD (observe AB = CD)

5. Join the radius to get the ΔOAB and ΔOCD .

6. Using trace paper, take the replicas of triangle ΔOAB and ΔOCD.

7. Place these triangles ΔOAB and ΔOCD one on the other.

Observation

1. What do you observe? Is ΔOAB ≡ ΔOCD ? Answer: Yes ΔOAB ≡ ΔOCD 

2. Construct perpendicular line to the chords AB and CD passing through the centre O. Measure the distance from O to the chords.

Now we are going to find out the length of the chords AB and CD, given the angles subtended by two chords at the centre of the circle are equal. That is, ∠AOB = ∠COD and the two sides which include these angles of the ΔAOB and ΔCOD are radii and are equal.

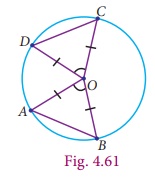
By SAS rule, ΔAOB ≡ ΔCOD . This gives chord AB = chord CD.

Now let us write the converse result as follows:

Converse of theorem 8

If the angles subtended by two chords at the centre of a circle are equal, then the chords are equal.

In the same way we are going to discuss about the distance from the centre, when the equal chords are given. Draw the perpendicular OL ⊥ AB and OM ⊥ CD. From theorem 7, these perpendicular divides the chords equally. So AL = CM . By comparing the ΔOAL and ΔOCM , the angles ∠OLA = ∠OMC = 90° and OA =OC are radii. By RHS rule, the ΔOAL ≡ ΔOCM . It gives the distance from the centre OL = OM and write the conclusion as follows.

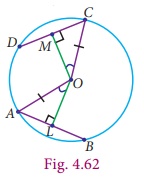
Theorem 9 Equal chords of a circle are equidistant from the centre.

Let us know the converse of theorem 9, which is very useful in solving problems.

Converse of theorem 9

The chords of a circle which are equidistant from the centre are equal.

3. Angle Subtended by an Arc of a Circle

Activity – 6

Procedure :

1. Draw three circles of any radius with centre O on a chart paper.

2. From these circles, cut a semi-circle, a minor segment and a major segment.

3. Consider three points on these segment and name them as A, B and C.

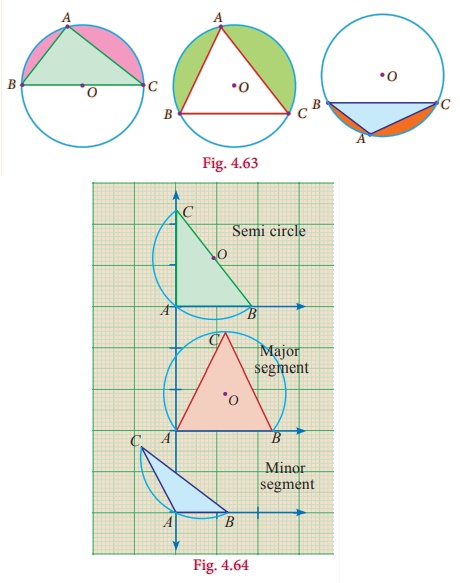
4. (iv) Cut the triangles and paste it on the graph sheet so that the point A coincides with the origin as shown in the figure.

Observation :

(i) Angle in a Semi-Circle is right angle.

(ii) Angle in a major segment is acute angle.

(iii) Angle in a minor segment is obtuse angle.

Now we are going to verify the relationship between the angle subtended by an arc at the centre and the angle subtended on the circumference.

4. Angle at the Centre and the Circumference

Let us consider any circle with centre O. Now place the points A, B and C on the circumference.

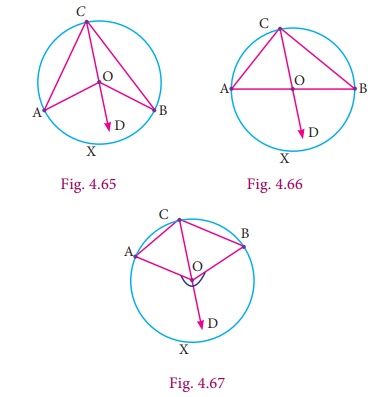
Here  is a minor arc in Fig.4.65, a semi circle in Fig.4.66 and a major arc in Fig.4.67.

The point C makes different types of angles in different positions (Fig. 4.65 to 4.67). In all these circles,  subtends ∠AOB at the centre and ∠ACB at a point on the circumference of the circle.

We want to prove ∠AOB =2∠ACB . For this purpose extend CO to D and join CD.

∠OCA = OAC since OA = OC (radii)

Exterior angle = sum of two interior opposite angles.

∠AOD = ∠OAC + OCA

= 2∠OCA .... (1)

Similarly,

∠BOD = ∠OBC + ∠OCB

= 2∠OCB .... (2)

From (1) and (2),

∠AOD + ∠BOD = 2(∠OCA + ∠OCB)

Finally we reach our result ∠AOB = 2∠ACB .

From this we get the result as follows :

Theorem 10

Progress Check

i. Draw the outline of different size of bangles and try to find out the centre of each using set square.

ii. Trace the given cresent and complete as full moon using ruler and compass.

Theorem 10

The angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Note

• Angle inscribed in a semicircle is a right angle.

• Equal arcs of a circle subtend equal angles at the centre.

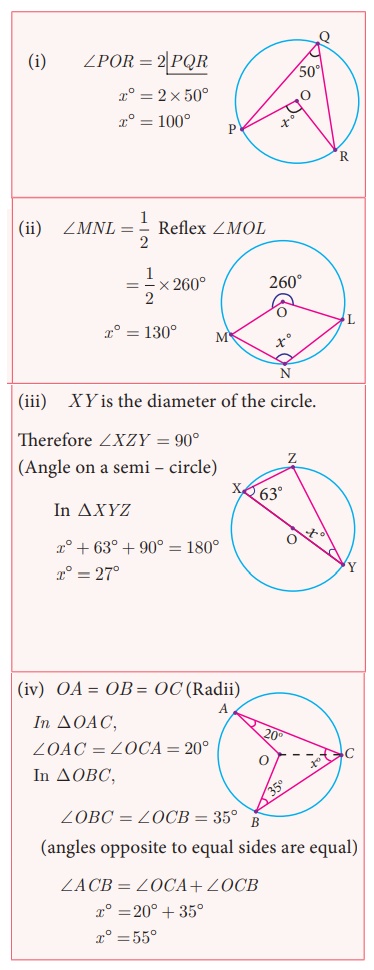
Example 4.7

Find the value of x° in the following figures:

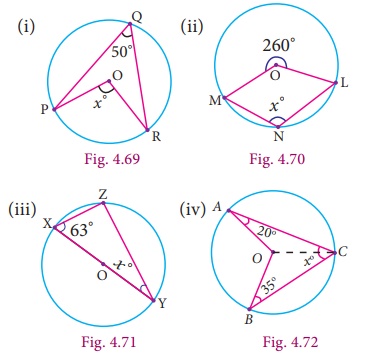
Solution

Using the theorem the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of a circle.

Example 4.8

If O is the centre of the circle and ∠ABC = 30° then find ∠AOC. (see Fig. 4.73)

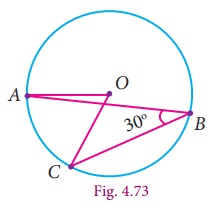
Solution

Given ∠ABC = 30°

∠AOC = 2∠ABC

(The angle subtended by an arc at the centre is double the angle at any point on the circle)

= 2×30°

= 60°

Now we shall see, another interesting theorem. We have learnt that minor arc subtends obtuse angle, major arc subtends acute angle and semi circle subtends right angle on the circumference. If a chord AB is given and C and D are two different points on the circumference of the circle, then find ∠ACB and ∠ADB . Is there any difference in these angles?

5. Angles in the same segment of a circle

Consider the circle with centre O and chord AB. C and D are the points on the circumference of the circle in the same segment. Join the radius OA and OB.

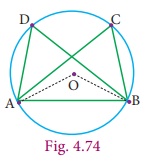
1/2 ∠AOB = ∠ACB (by theorem 10)

and

1/2 ∠AOB = ∠ADB (by theorem 10)

∠ACB = ∠ADB

This conclusion leads to the new result.

Theorem 11 Angles in the same segment of a circle are equal.

Example 4.9

In the given figure, O is the center of the circle. If the measure of ∠OQR= 48° , what is the measure of ∠P ?

Solution

Given ∠OQR= 48° .

Therefore, ∠ORQ also is 48° . (Why?__________)

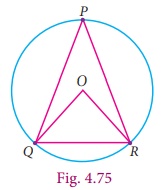
∠QOR =180° −(2×48°)=84° .

The central angle made by chord QR is twice the inscribed angle at P.

Thus, measure of ∠QPR = 1/2 × 84°= 42° .